Изучение основных способов представления математических проблем в символьном виде, пригодном для формальной обработки на компьютере

Министерство Общего и Профессионального Образования

НГТУ

Лабораторная работа №1

по дисциплине «Системы искусственного интеллекта»

Факультет:         ПМИ

Группа:               ПМ-83

Студенты:           Большакова А

Миркин Е.

Журавлев В.

Моисеев Д.

Преподаватели:

г. Новосибирск 2001

1.Цель работы:

Изучение основных способов представления математических проблем в символьном виде, пригодном для формальной обработки на компьютере.

2.Задание

Используя в качестве прототипа программу аналитического дифференцирования, составить программу аналитического интегрирования математических выражений.

3. Решение

Расширение структуры данных:

Так как неопределённый интеграл может содержать такие функции как arctg, arcsin,  модуль, а так же вещественные и комплексные числа, то необходимо расширить структуру данных для представления математических выражений

EXP=var(STRING); int(INTEGER); plus(EXP,EXP); minus(EXP,EXP); mult(EXP,EXP);  div(EXP,EXP); ln(EXP); cos(EXP); sin(EXP); tan(EXP); sec(EXP); potens(EXP,EXP)

следующим образом:

EXP=var(STRING); flt(REAL); plus(EXP,EXP); minus(EXP,EXP); mult(EXP,EXP); div(EXP,EXP); ln(EXP); cos(EXP); sin(EXP); tan(EXP); potens(EXP,EXP); abs(EXP); atan(EXP); asin(EXP)

Поддержка вещественных чисел:

Для реализации корректного преобразования вещественных чисел, требуется

а) модифицировать сканер исходной программы следующим образом:

праило    elmexp([TALSTR|IL],IL,int(INT)):-str_int(TALSTR,INT),!.

заменить на правила:

elmexp([S1,".",S2|IL],IL,flt(FLT)):-concat(S1,".",S3), concat(S3,S2,S4),

                        str_real(S4,FLT),!.

                elmexp([STR|IL],IL,flt(FLT)):-str_real(STR,FLT),!.

б) модифицировать блок преобразования внутреннего представления выражения во внешнее строковое:

заменить правило strexp(int(INT),INTSTR) :- str_int(INTSTR,INT).

на правило             strexp(flt(FLT),FLTSTR) :- str_real(FLTSTR,FLT).

в) заменить все вхождения элемента int() на flt() и все вызовы предиката str_int() на вызовы str_real().

Поддержка комплексных чисел:

Для обеспечения поддержки комплексных чисел, объявим переменную i как мнимую единицу и к правилам редуцирования математического выражения добавим правила, соответствующие свойствам i²=-1, i³-i, i⁴=1, i⁵=i,…

multr(var(i),var(i),flt(-1)):-!.

multr(var(i),X,R):-multr(X,var(i),R),!.

multr(mult(X,var(i)),var(i),M1):-!, multr(flt(-1),X,M1).

multr(var(i),mult(X,var(i)),M1):-!, multr(flt(-1),X,M1).

multr(mult(X,var(i)),mult(Y,var(i)),mult(flt(-1),R)):-!, multr(X,Y,R).

multr(mult(X,var(i)),Y,mult(R,var(i))):-!, multr(X,Y,R).

multr(var(i),X,mult(X,var(i))):-!.

а так же в остальных правилах переменную i всегда считать константой.

Интегрирование:

Введём предикат интегрирования:

i(EXP,EXP,EXP)

i(U,X,V) Þ

Теперь можно определить правила нахождения интеграла:

1.  Свойства интеграла:

i(plus(U,V),X,plus(U1,V1)):-i(U,X,U1), i(V,X,V1), !.

i(minus(U,V),X,minus(U1,V1)):-i(U,X,U1), i(V,X,V1), !.

,  С = const

i(mult(E,U),X,mult(E,V)):- const(E,X), i(U,X,V), !.

      i(mult(U,E),X,mult(E,V)):- const(E,X), i(U,X,V), !.

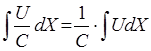, С=const

i(div(E,U),X,mult(E,V)):- const(E,X), i(div(flt(1),U),X,V), !.

      i(div(U,E),X,mult(div(flt(1),E),V)):- const(E,X), i(div(flt(1),U),X,V), !.

2.  Интегралы от рациональных функций:

i(E,X,mult(E,X)):-const(E,X), !.

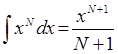, N¹-1

i(X,X,div(potens(X,flt(2)),flt(2))):-!.

i(potens(X,flt(N)),X,div(potens(X,flt(M)),flt(M))):-N<>-1, M=N+1, !.

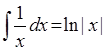
i(potens(X,flt(-1)),X,ln(abs(X))):-!.

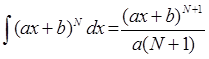
i(potens(plus(mult(A,X),B),flt(N)),X,div(potens(plus(mult(A,X),B),flt(M)),

mult(A,flt(M)))):-N<>-1,M=N+1,const(A,X), const(B,X),!.

i(potens(plus(mult(X,A),B),flt(N)),X,div(potens(plus(mult(A,X),B),flt(M)),

mult(A,flt(M)))):-N<>-1,M=N+1,const(A,X), const(B,X),!.

i(potens(plus(B,mult(A,X)),flt(N)),X,div(potens(plus(mult(A,X),B),flt(M)),

mult(A,flt(M)))):-N<>-1,M=N+1,const(A,X), const(B,X),!.

i(potens(plus(B,mult(X,A)),flt(N)),X,div(potens(plus(mult(A,X),B),flt(M)),

mult(A,flt(M)))):-N<>-1,M=N+1,const(A,X), const(B,X),!.

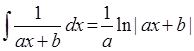
i(div(flt(F),plus(mult(A,X),B)),X,mult(div(flt(F),A),ln(abs(plus(mult(A,X),B))))):-                          сonst(A,X), const(B,X),!.

i(div(flt(F),plus(mult(X,A),B)),X,mult(div(flt(F),A),ln(abs(plus(mult(A,X),B))))):-const(A,X), const(B,X),!. 

i(div(flt(F),plus(B,mult(A,X))),X,mult(div(flt(F),A),ln(abs(plus(mult(A,X),B))))):-const(A,X), const(B,X),!. 

i(div(flt(F),plus(B,mult(X,A))),X,mult(div(flt(F),A),ln(abs(plus(mult(A,X),B))))):-const(A,X), const(B,X),!.

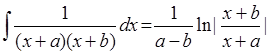
i(div(flt(F),mult(plus(X,A),plus(X,B))),X,mult(div(flt(F),minus(A,B)),ln(abs(

div(plus(X,B),plus(X,A)))))):-const(A,X), const(B,X),not(equal(A,B)), !.

i(div(flt(F),mult(plus(A,X),plus(X,B))),X,mult(div(flt(F),minus(A,B)),ln(abs(