Изучение методов, разработка алгоритмов и программной имитации непрерывных псевдослучайных величин с произвольным законом распределения, страница 2

4. Написать алгоритм моделирования случайной величины x, распределенной с плотностью f(x)

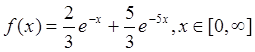
Решение.

Плотность случайной величины представима в виде ,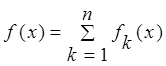

Воспользуемся утверждением 1 и получим:

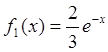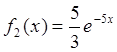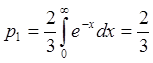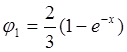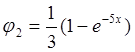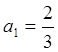,  , , , , , , ,  и т.д. Значит, схема моделирования случайной величины следующая

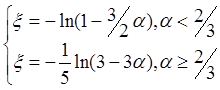; где .

Тест

N=2000, r=30, 3.78.

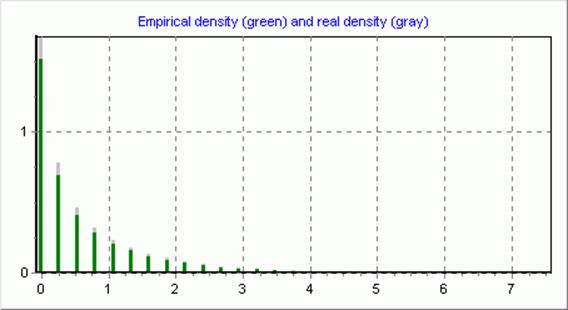
Вывод: выборка имеет заданное распределение.

Первые элементы выборки:

0.1597015           0.02101544         1.741642             0.9155036           0.4694039           0.1620339           0.3782876               0.1017856           3.661663             1.383151             0.7426272           0.3553693           0.07694106         0.2395295               0.05695766         2.290665             1.119972             0.5953739           0.2530858           1.172283             0.1583078               0.02031761         1.732704             0.9115819           0.466892             0.1601863           0.3741609           0.1007421               3.602263             1.376902             0.7393294           0.3531294           0.07524523         0.2374582           0.05612381               2.27526                1.115169             0.592529             0.2510649           1.023594             0.1569264           0.0196236               1.723864             0.9076834           0.4643915           0.1583458           0.3701255           0.09970604         3.546303               1.370704             0.7360489           0.350899             0.07355565         0.2354123           0.05529509         2.260118               1.110398             0.5896978          

5. Написать алгоритм моделирования случайной величины x с заданной плотностью распределения по методу суперпозиции.

Плотность задана так: .

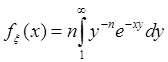Решение.

Пусть ,

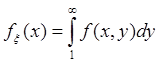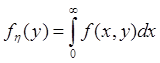
  из выражения для заданной плотности находим

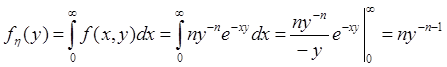
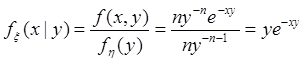
Процесс моделирования

1.

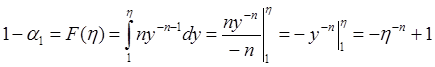
т.е. ,   ,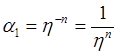 

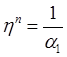2. 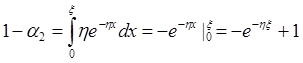                                т. к. .

        .

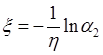Итак :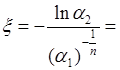 

Тест

N=2000, r=30, 18.10

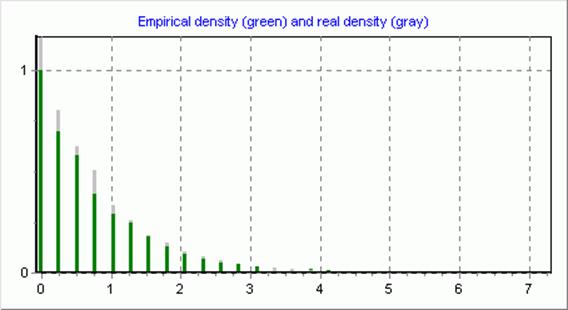
Элементы выборки:

0.2721332           0.1633788           1.188366             0.5668168           0.9112875           1.723496             0.6872023               0.19311 1.048519             0.06430663         0.741545             1.176046             1.107752             0.01098072         0.6838265               0.2996131           0.6545778           0.5624471           1.198602             1.263275             0.9344102           1.768769               0.08795114         0.6792499           1.152059             1.085624             0.1737523           0.126629             1.468725               1.23407 0.439898             0.1747595           0.7737429           0.08270433         0.1725813           2.443594             2.889162               0.6137377           0.6748349           0.6634058           0.2662614           0.01031313         0.263178             3.221441               1.663449             0.3609554           2.114456             1.867849             0.6545748           0.8968812           0.07351699               2.979102             1.612334             1.415288             0.5489823           0.1866001           0.2755638           0.4459786               0.1762539           0.9120706           0.6644788           0.07775007         0.9200639          

Гипотеза о виде распределения принимается.

Значения функции распределения были получены численно, методом трапеций следующим образом:

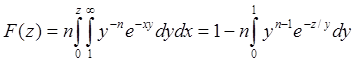, отрезок [0,1] в этом примере разбивался на 300 точек.

График плотности был построен на основе вычисления интеграла по схеме Монте-Карло

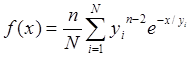 , где .

6. Написать алгоритм моделирования случайной величины x с заданной плотностью распределения по методу исключения.

Плотность .

Решение.

Для того, чтобы  была плотностью, необходимо 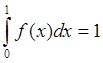. Это выполняется при .

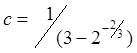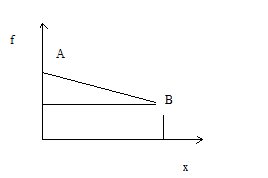
Алгоритм моделирования случайной величины:

1.  Генерируется случайная точка .

2.  Генерируется случайная точка .

3.  Производится проверка : если h<f(x), то h принимается за значение случайной величины, иначе– переход на первый пункт.

Тест

N=4000, r=30, 6.846

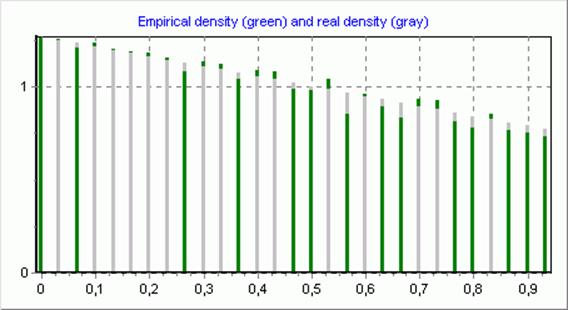
Гипотеза о виде распределения принимается.

Элементы выборки:

0.699915             0.39979 0.24975 0.09972507         0.9497151           0.7996201           0.4994752           0.3494253               0.1993903           0.04937038         0.7492755           0.599206             0.4491407           0.2990957           0.1490658               0.9990509           0.848951             0.5487962           0.3987414           0.09867662         0.648492             0.4984272               0.3483773           0.1983425           0.04832266         0.8983178           0.748228             0.5981532           0.4480934               0.2980486           0.1480187           0.9980039           0.8479041           0.5477496           0.3976948           0.247655               0.09763026         0.7975257           0.647446             0.1972968           0.04727704         0.8972723           0.7471826               0.5971079           0.2970035           0.1469738           0.8468594           0.6967747           0.546705             0.3966503               0.2466107           0.096586             0.9465763

Комбинированное использование линейного и стандартного генератора.