Изучение методов, разработка алгоритмов и программной имитации непрерывных псевдослучайных величин с произвольным законом распределения

МО И ПО РФ

НГТУ

КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ

ЛАБОРАТОРНАЯ  РАБОТА №3

ПО

²МЕТОДАМ МОДЕЛИРОВАНИЯ²

Факультет ПМИ

Группа ПМ-83

Студентки

          Гламаздина О.Н.

          Лях К.Н.

Преподаватели 

          Тишковская С.В.

          Тимофеев В.С.

Новосибирск 2001

МОДЕЛИРОВАНИЕ ПРОИЗВОЛЬНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Цель работы

Изучение методов, разработка алгоритмов и программной имитации непрерывных псевдослучайных величин с произвольным законом распределения. Статистический анализ качества псевдослучайных последовательностей.

Вариант 1

Введем обозначения :

N-объем выборки;

r –количество интервалов группирования;

- значение статистики 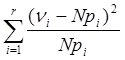, – количество элементов выборки, попавших в i-ый интервал разбиения  области определения; ,i=0,1..N.

Поскольку ниже будет приведены тесты для r=30, то сразу определим квантиль порядка (1-a) при a=0.1  

=39.087.

1.  Найти методом обратной функции моделирующее выражение для случайной величины x, имеющей плотность распределения

.

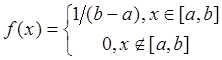Функция распределения заданной непрерывной случайной величины 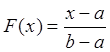. Находим случайную величину x из равенства  , где :

.

Ответ: моделирующее выражение для случайной величины , .

Тест

a=1, b=3.5, N=2000, r=30, значение статистики c²=0.365

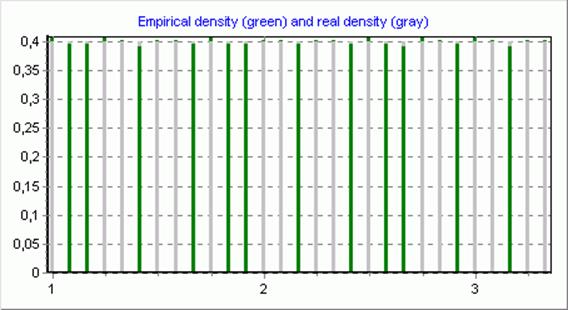
Некоторые элементы выборки:

2.875181             2.499993             2.124843             1.749731             1.374656            

3.499618             3.124368             2.749156             2.373981             1.998844             1.623744             1.248681               3.373656             2.998419             2.623219             2.248057             1.872932             1.497845             1.122795               3.247783             2.872558             2.497371             2.122221             1.747109             1.372034             3.496997               3.121747             2.746535             2.37136                1.996223             1.621124             1.246061             3.371037               2.9958                  2.6206                  2.245438             1.870314             1.495227             1.120177             3.245165               2.86994                2.494753             2.119604             1.744492             1.36941

Гипотеза о виде распределения принимается.

Для моделирования равномерных на (0,1) случайных величин использовалась линейная конгруэнтная схема.

2. Найти моделирующее выражение для случайной величины x, имеющей заданную плотность распределения, по методу обратной функции, когда  немонотонна .

Плотность задана функцией .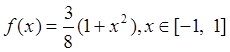

Решение.

Плотность случайной величины представима в виде 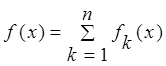, . Строить моделирующую формулу будем на основе следующего

утверждения 1:

Пусть 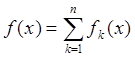, . Обозначим , , ,  ,

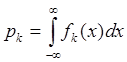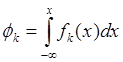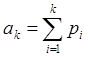Случайная величина , при  имеет плотность распределения .

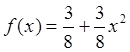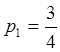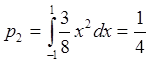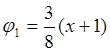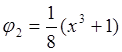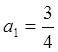, , , , , , , , откуда имеем  моделирующее выражение для случайной величины x:

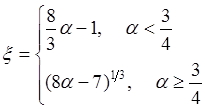, где

Тесты:

N=2000,r=30, c²=1.277

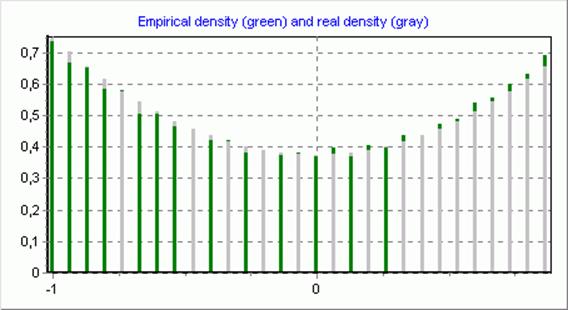
Некоторые элементы выборки:

-0.5848035         0.86644                0.4662534           0.06610673         -0.3339999          0.7340665           0.8423633               -0.8448543          0.7321071           0.3319339           0.0681993           -0.4682925          -0.8683457          0.5798132               0.998068             0.5978682           0.1977084           -0.2024113          -0.6024911          0.9974627           -0.592871               0.863643             0.4634566           0.0633103           -0.336796            -0.7368624          0.838405             -0.8487525               0.7293121           0.3291391           -0.07099377       -0.4710867          -0.8711396          0.5713813           0.9952747               0.5950751           0.1949156           -0.2052039          -0.6052833          0.9946486           -0.6007092          0.8608516               0.4606655           0.06051946         -0.3395866

Гипотеза о виде распределения принимается.

3. Написать алгоритм моделирования случайной величины x, распределенной с плотностью f(x) , с использованием порядковых статистик.

Плотность задана функцией .

Решение.

Воспользуемся утверждением 2:

Пусть  имеет вид , где n, k – некоторые натуральные числа. Тогда x – k –я порядковая статистика для выборки  , . Моделирование случайной величины сводится к моделированию  с последующим упорядочиванием их, так что .

В нашем примере k=2, n=4, т.е. плотность распределения случайной величины представима в виде . Вывод: случайная величина x равна второй порядковой статистике  выборки  , . 

Тест

N=2000, r=30, c²=16.84

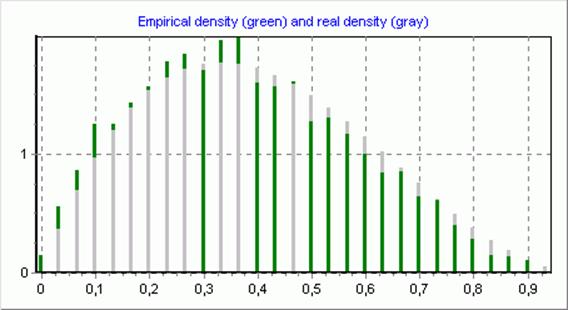
Гипотеза о виде распределения принимается.

Последовательность равномерных случайных величин получали стандартным генератором.

Некоторые элементы полученной выборки:

0.5809198           0.4497818           0.2816248           0.2057199           0.1265297           0.6338084           0.3105258               0.4712058           0.03311258         0.3054215           0.155391             0.1626637           0.5252846           0.6099124               0.494583             0.4262215           0.3848994           0.1050973           0.2375561           0.2131718           0.2810144               0.5048453           0.4300058           0.2047593           0.4037904           0.8076418           0.7546429           0.5565966               0.454507             0.721305             0.1544311           0.0369274           0.4797205           0.1329997           0.5145116               0.4133427           0.4180425           0.2188177           0.7014374           0.1438337           0.5700552           0.5038864               0.7252419           0.3567614           0.05378027         0.8345897           0.7536845           0.2551653           0.131138               0.5822321           0.1534731           0.2363048