Вопросы экзаменационных билетов по теории вероятности

Вопросы экзаменационных билетов

1.  Определение  с.ф. СП. Вероятностные характеристики СП. На какие два класса можно разбить СП в зависимости от распределения СП.

2.  Моменты с.ф. выражение моментов второго порядка через двумерную плотность вероятности. Дисперсия с.ф., интегральное выражение для нее. Свойства моментов второго порядка.

3.  Марковские процессы. Каким конечномерным распределением определяется вся последовательность конечномерных распределений МП? Приведите иное определение МП - в терминах конечномерных распределений.

4.  Гауссовские процессы: определение, различные формы записи распределений гауссовского СП. Структура вынужденного гауссовского распределения. Существует ли гауссовская с.ф., определенная на заданном параметрическом множестве Т и такая, что ее характеристики совпадают с заданными вектором а и неотрицательно определенной матрицей R, размерности n и nxn соответственно?

5.  Стационарные процессы: стационарность в узком смысле, стационарность в широком смысле, какое из этих двух понятий содержит в себе другое?

6.  Процессы с некоррелированными приращениями (СПНКП). Описание СПНКП.

7.  Процессы с независимыми приращениями (СПНП). Многомерные распределения СПНП. Является ли СПНП Марковским? СПНКП?

8.  Пуассоновский процесс с параметром l. Физический смысл параметра l. Является ли пуассоновский процесс СПНКП? Марковским? Что можно сказать о траектории пуассоновского процесса?

9.  Винеровский процесс. Многомерные распределения винеровского процесса. Можно ли назвать винеровский процесс Марковским? Можно ли назвать винеровский процесс процессом со стационарными приращениями? Многомерные винеровские процессы.

10.  Последовательности случайных величин (с.в.). различные виды сходимости. Сходимость в среднем квадратическом. Связь между различными видами сходимости. Лемма Лоэва. Следствия.

11.  Утверждение обратное по отношению к лемме Лоэва. Стохастический критерий Коши с.к. сходимости.

12.  С.к. непрерывность с.ф. необходимые и достаточные условия с.к. непрерывности.

13.  О непрерывности ковариационной функции на квадрате TxT. Является ли винеровский процесс с.к. непрерывным?

14.  Пусть  - винеровский скалярный, стандартный процесс. Доказать, что существует 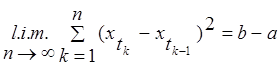. Что можно сказать о реализации винеровского процесса?

15.  Дифференцирование с.ф. необходимые и достаточные условия дифференцируемости. Выражения для .

16.  Является ли СПНКП с.к. дифференцируемым? Слабо с.к. дифференцируемым? Является ли винеровский процесс с.к. дифференцируемым?

17.  Интегрируемость с.ф. необходимое и достаточное условие интегрируемости. Вывести одну из формул:  , если Y(t) с.к. интеграл процесса X(t), tÎT, с весом g(t,T).

18.  Частные случаи с.к. интеграла от  процесса X(t). Интеграл с переменным верхним пределом интегрирования. Формула интегрирования по частям. Является ли с.к. интегрируемым винеровский процесс?

19.  Слабая с.к. сходимость. Белый шум. Интегралы, содержащие белый шум. Ковариационная функция такого интеграла.

20.  Эргодические СП. Необходимые и достаточные условия эргодичности СП. Как выглядит определение эргодического СП относительно его дисперсии. Что это означает для практики?

21.  Стохастический интеграл по скалярному СП. Необходимое и достаточное условие существования интеграла. Обобщение понятия стохастического интеграла на случай n- мерного СП. Связь стохастического и с.к. интегралов. Что изменится, если процесс в определении стохастического интеграла не будет СПНКП?

22. Стохастический интеграл, как интеграл, содержащий белый шум. Какие процессы представимы в виде таких интегралов?