Вопросы экзаменационных билетов по теории вероятности, страница 2

23. Стохастические интегралы от неслучайных функций векторного переменного. Необходимые о достаточные условия существования интеграла. Каноническое представление стохастического интеграла. Можно ли считать стохастический интеграл по скалярному СП интегралом по стохастической мере?

24. Интеграл Ито. Необходимые и достаточные условия существования интеграла Ито. Другие виды стохастических интегралов от случайных функций. Математическое ожидание и дисперсия для интеграла Стратоновича.

25. Определение стационарных случайных функций (с.с.ф.). Некоторые их свойства. Верно ли утверждение, что значение  с.с.ф. и ее производной не коррелированны?

26. Стационарные с.ф. с дискретным спектром. В каком случае ковариационную функцию стационарного СП можно считать суммой ряда Фурье? Каков смысл коэффициентов этого ряда Фурье? Сформулировать условия, при которых стационарный СП представлен рядом Фурье.

27. Интегральная форма записи стационарного СП и его ковариационной функции. Необходимые и достаточные условия существования стохастического интеграла, определяющего стационарный СП. Интенсивность СПНКП в стохастическом интеграле, определяющем ССП. Как называют стохастический интеграл, определяющий ССП? В каком случае ССП  можно рассматривать как процесс с непрерывным спектром?

28. Свойства спектральной плотности. Любая ли с.с.ф. может быть представлена спектральным разложением?

29. Стационарный белый шум. Модели стационарного белого шума.

30. Связь частных характеристик процесса , и процессов , .

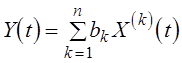31. Как связаны вероятностные характеристики входного и выходного случайных процессов при прохождении входного процесса через линейную динамическую систему. Можно ли вычислить эти характеристики иным путем (не опираясь на спектральные плотности)?

- 4 32. Марковские процессы с дискретными состояниями. Марковские цепи. Характеристики Марковских цепей: матрица переходных вероятностей, ее свойства, вектор вероятностей состояний. Граф состояний, размеченный граф состояний. Однородные Марковские цепи.

33. Марковские процессы с дискретными состояниями и непрерывным временем. Уравнения Колмогорова для вероятностей состояний. Задача Коши для матричного уравнения Колмогорова. Вектор предельных вероятностей состояний системы.

34. Процесс гибели - размножения и циклический процессы.

35. Стохастические модели состояния. Требования к процессу случайных возмущений. Любой ли СП можно полагать в качестве процесса случайных возмущений?

36. Стохастическая задача Коши и ее решение (линейный и нелинейный случай).

37. Стохастические интегралы и дифференциалы в форме Ито и Стратоновича. Правило дифференцирования Ито.

38. Марковские процессы с непрерывными состояниями. Общие свойства Марковских процессов. Уравнения Колмогорова.

39. Вывод первого уравнения Колмогорова.

40. Вывод второго уравнения Колмогорова.

41. Стохастические модели состояния и уравнения Колмогорова.

42. Постановки задач для нахождения условной функции плотности вероятностей.

43. Вероятность пребывания Марковского процесса в заданной области.

44. Закон распределения времени пребывания МП в заданной области.

45. Среднее число выбросов значений МП за данный уровень.

46. Статистические моменты СП.

47. Постановка задачи оценивания параметров СП. Эффективные оценки. Неравенство Рао - Крамера.

48. Единственность решения задачи оценивания параметров СП (условия для функции плотности вероятностей, условия для математического ожидания и ковариационной матрицы).

49. Метод максимального правдоподобия.

50. Метод наименьших квадратов.

51. Задача параметрической идентификации стохастической модели состояния.

52. Задача оценивания параметров стохастических моделей состояния при наличии ошибок измерений. Фильтр Калмана.