Анализ данные при варьировании коэффициентов матрицы Брайсона

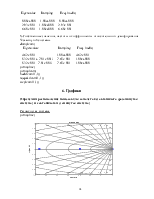
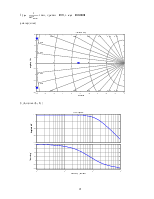
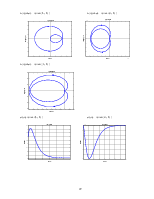
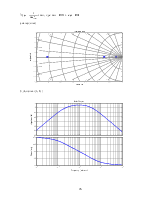
Построим логарифмические амплитудно-фазовые частотные характеристики для замкнутой системы (каждой из переменных ее состояния), для рассматриваемых регулируемых величин (угол отклонения руля высоты)

по скороподъемности

bode(zam(1,1))

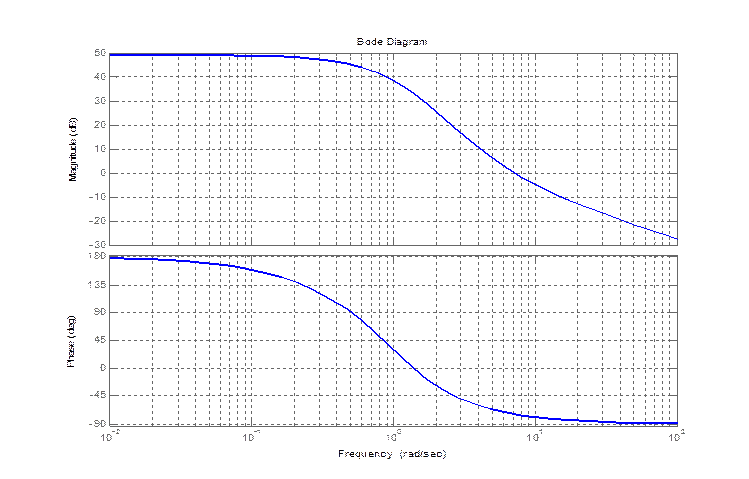
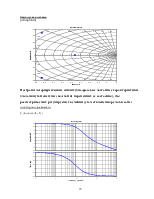
по углу атаки

bode(zam(2,1))

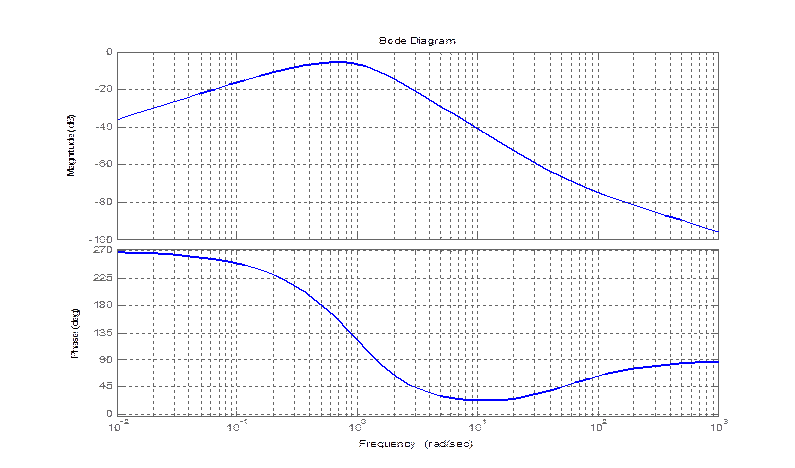
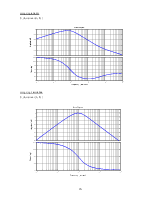
по углу тангажа

bode(zam(3,1))

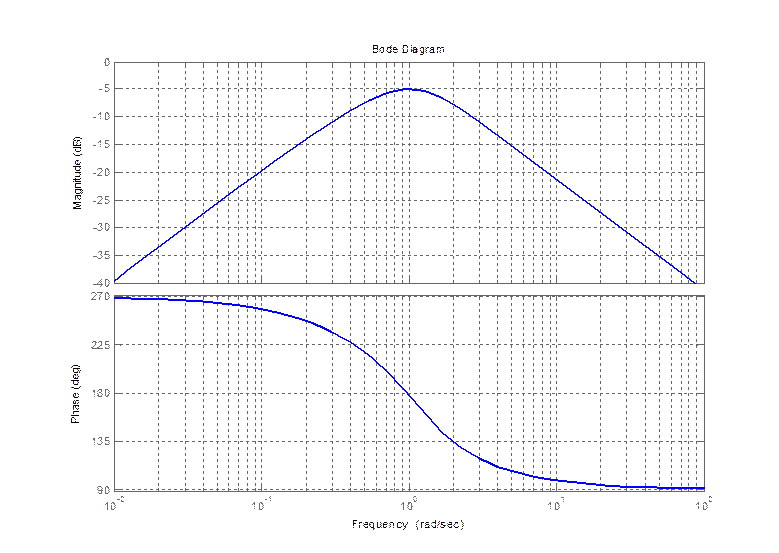
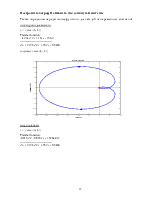
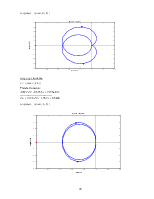
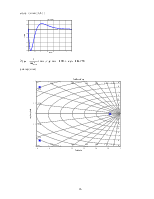
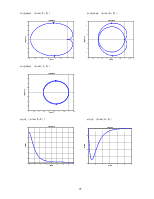
Построим годограф Найквиста для замкнутой системы

Также определим передаточные функции для каждой из переменных состояния

по скороподъемности

tf (zam(1,1))

Transfer function:

4.214 s^2 + 1.151 s - 156.2

---------------------------------s^3 + 2.126 s^2 + 1.952 s + 0.5466

nyquist(zam(1,1))

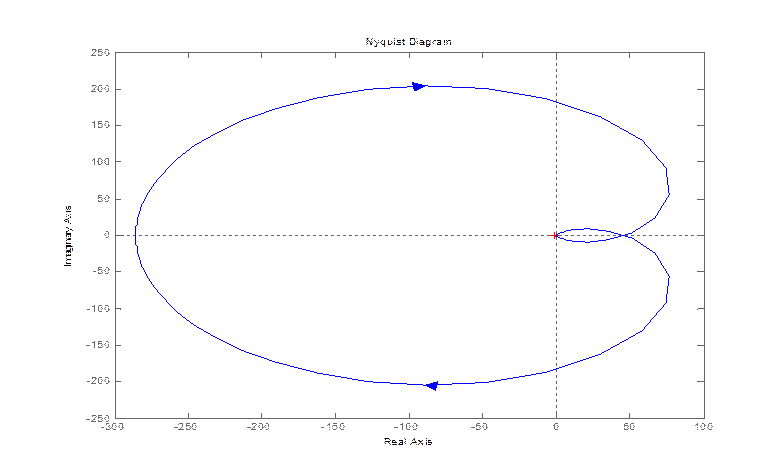
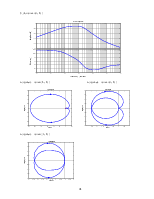
по углу атаки

tf (zam(2,1))

Transfer function:

-0.016 s^2 - 0.8767 s + 1.578e-017

---------------------------------s^3 + 2.126 s^2 + 1.952 s + 0.5466

nyquist (zam(2,1))

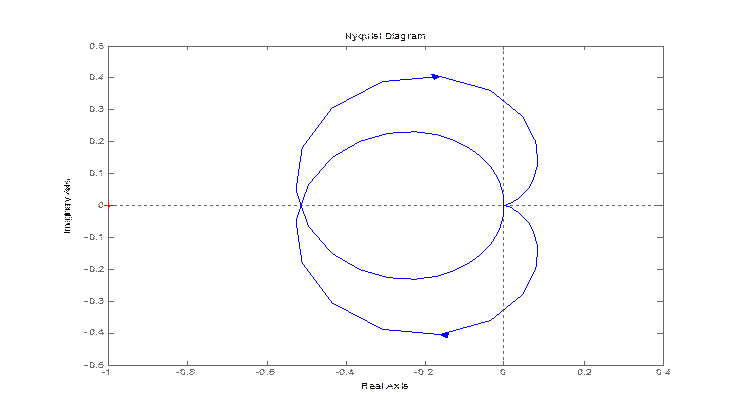
по углу тангажа

tf (zam(3,1))

Transfer function:

-0.872 s^2 - 0.5755 s + 2.795e-017

---------------------------------s^3 + 2.126 s^2 + 1.952 s + 0.5466

nyquist (zam(3,1))

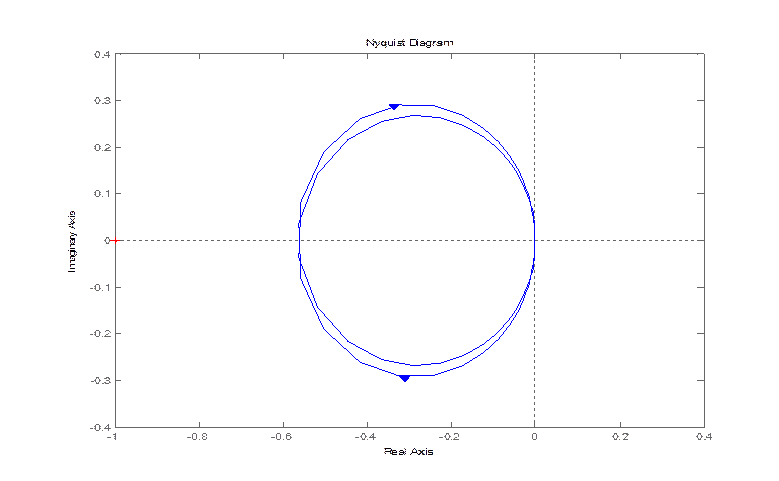
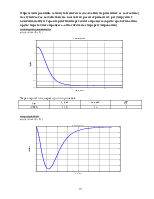
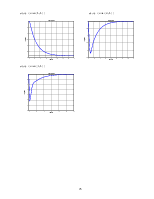
Определим реакцию замкнутой системы (каждой из переменных ее состояния) на ступенчатое воздействие по каждой из рассматриваемых регулируемых величин, найдем характеристики переходного процесса(время срабатывания, время переходного процесса, относительное перерегулирование)

по скороподъемности

step(zam(1,1))

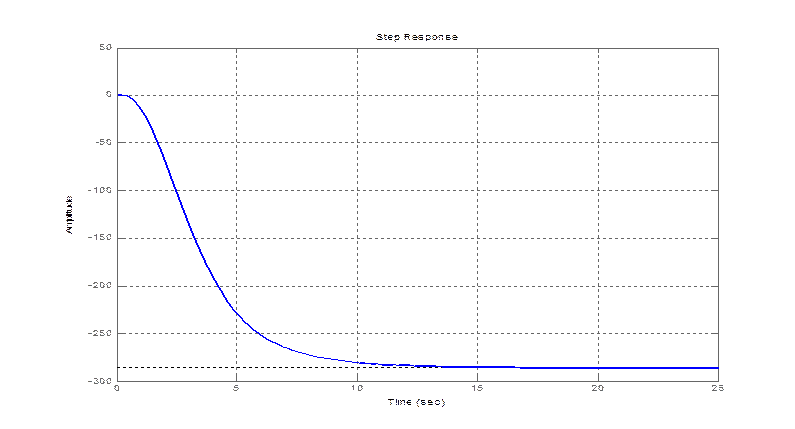
Характеристики переходного процесса:

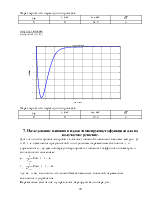
по углу атаки

step(zam(2,1))

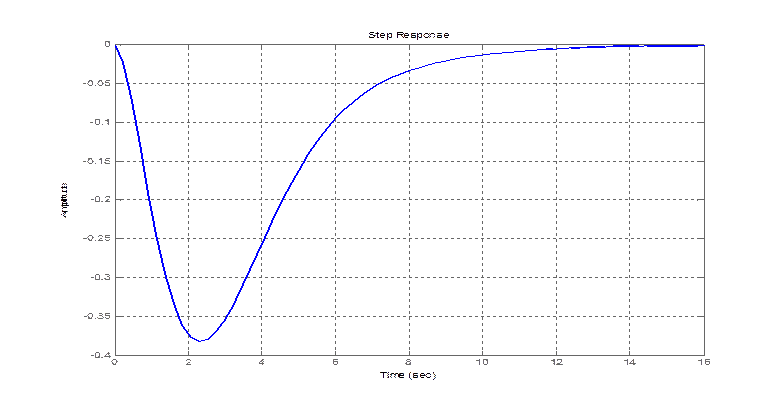
Характеристики переходного процесса:

по углу тангажа

step(zam(3,1))

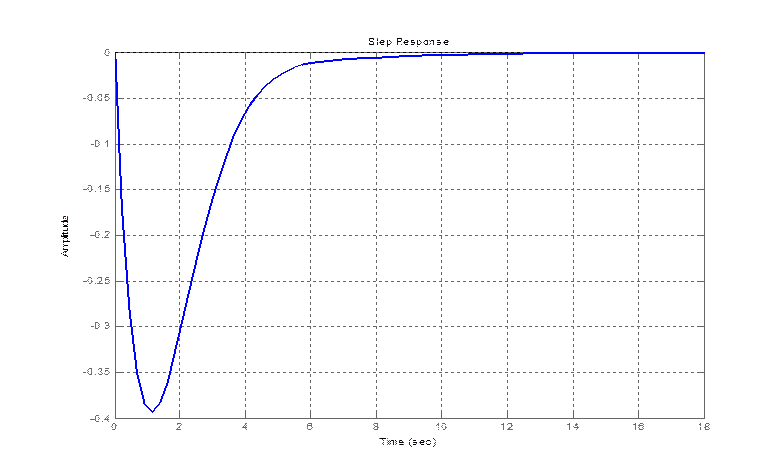
Характеристики переходного процесса:

7. Исследование влияния вида оптимизирующего функционала на получаемое решение.

Для того чтобы проанализировать влияние значений компонент весовых матриц   и , т. е. изменения предпочтений по отдельным переменным состояния  и управления , будем поочередно варьировать значения коэффициентов матриц и согласно соотношениям:

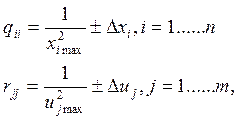
где  и  величины отклонений максимальных значений переменных состояния и управления.

Переменные состояния и управления варьируются поочередно.

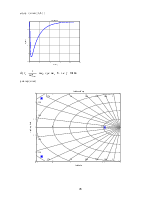
1) 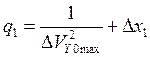, где , т. е

pzmap(zam)

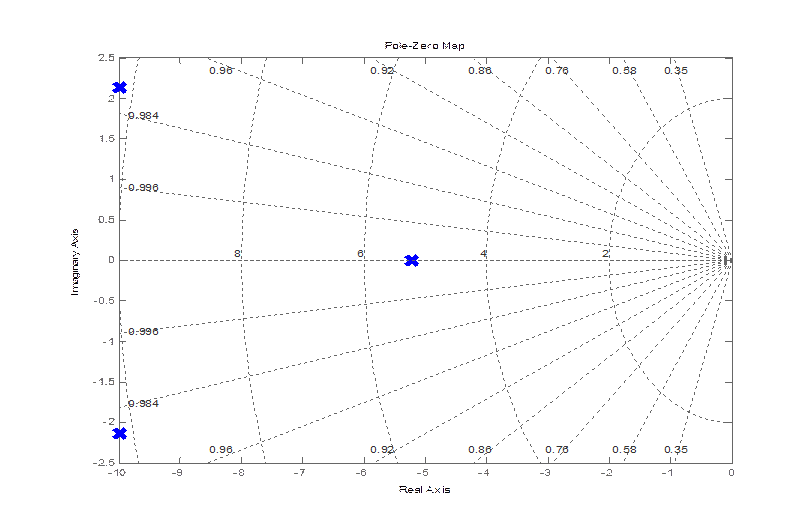
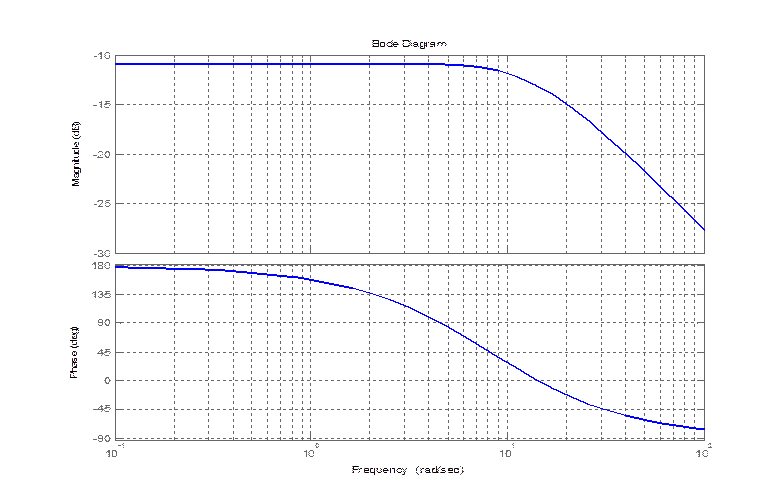
bode(zam(1,1))

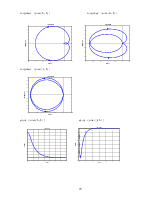
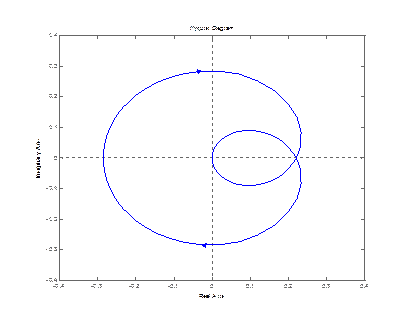
nyquist (zam(1,1))                                                   nyquist (zam(2,1))

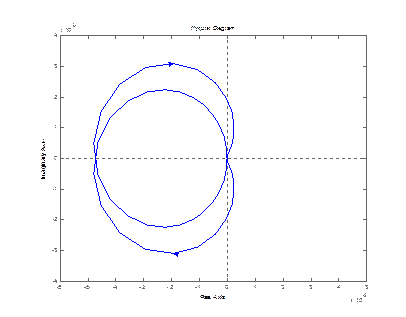
nyquist (zam(3,1))

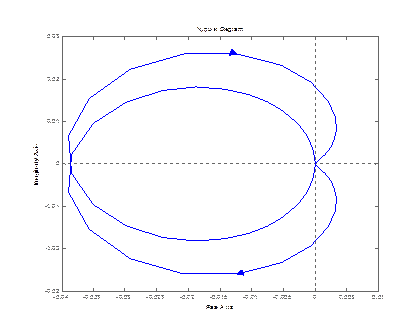
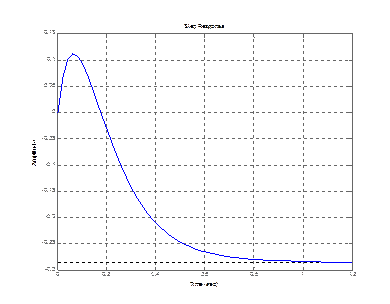
step(zam(1,1))                         step (zam(2,1))

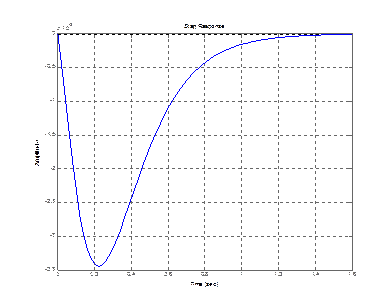
step (zam(3,1))

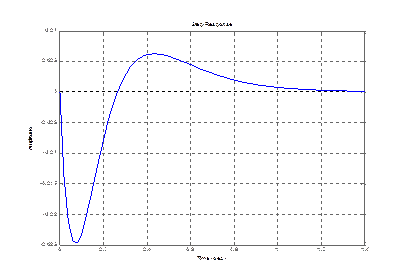
2) 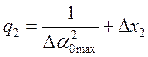, где , т. е

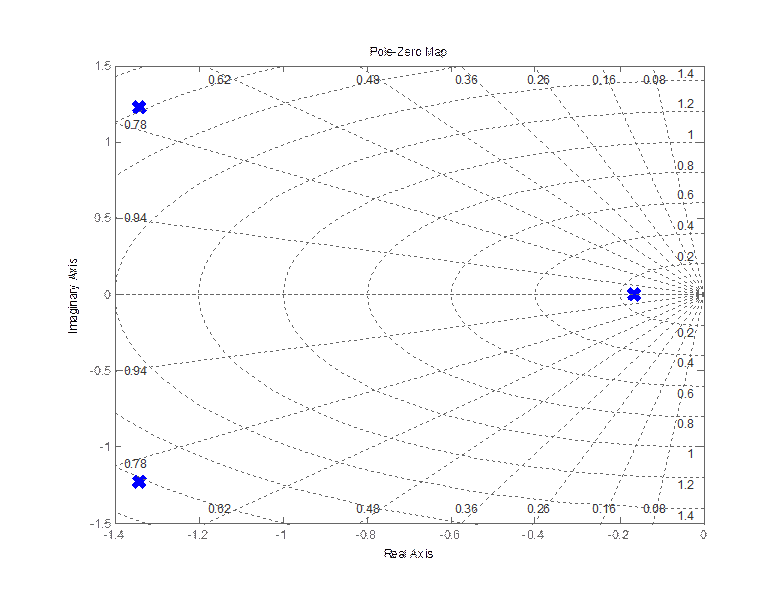
pzmap(zam)

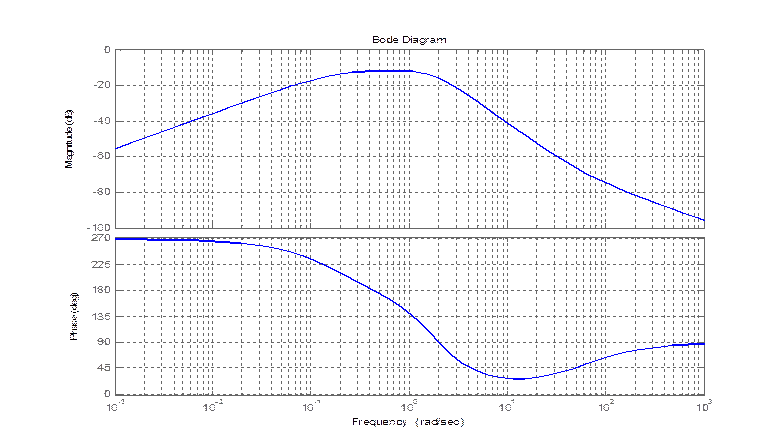
bode(zam(2,1))

nyquist (zam(1,1))                     nyquist (zam(2,1))

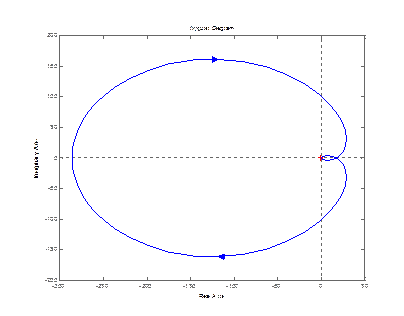
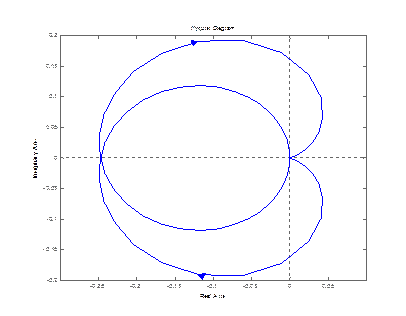
nyquist (zam(3,1))

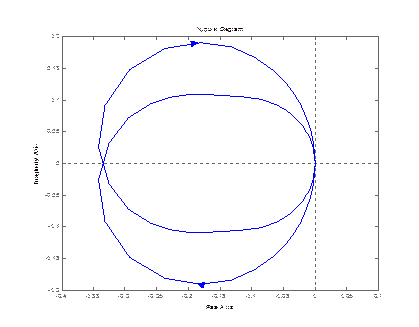
step (zam(1,1))                        step (zam(2,1))

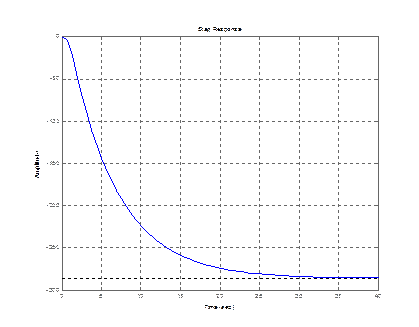
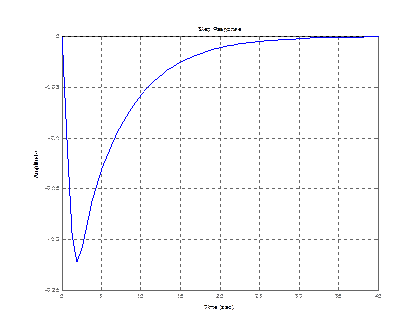
step (zam(3,1))

3) 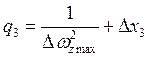, где , т. е

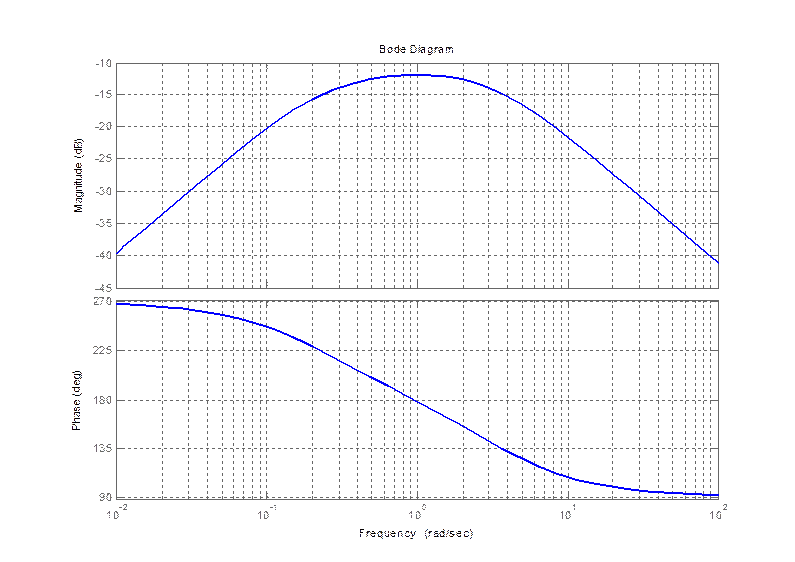
pzmap(zam)

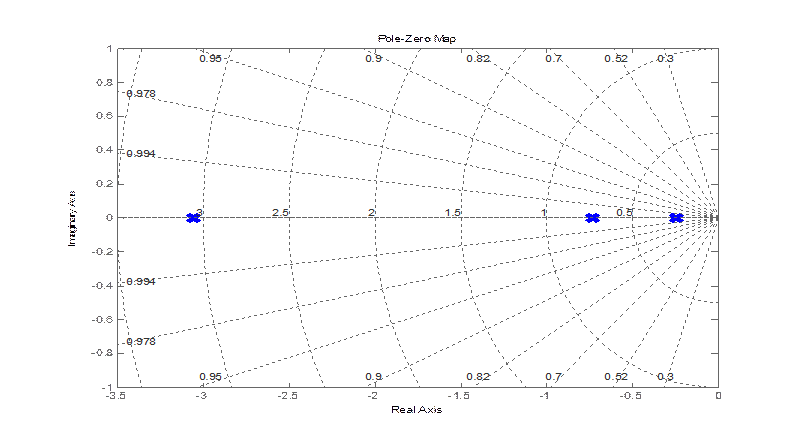
bode(zam(3,1))

nyquist (zam(1,1))                     nyquist (zam(2,1))

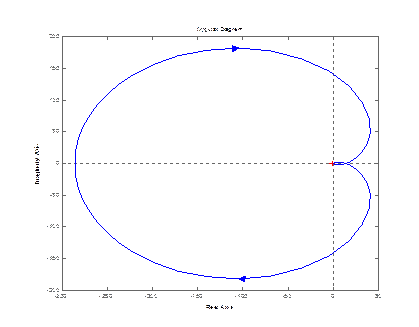
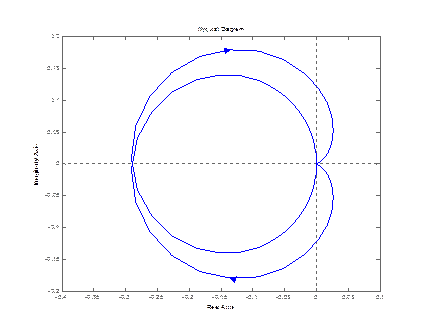
nyquist (zam(3,1))

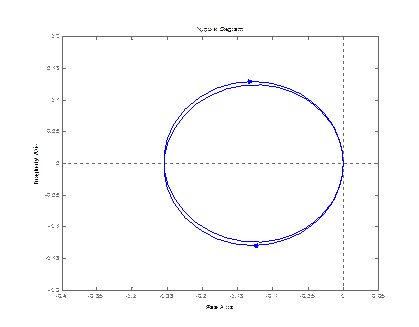
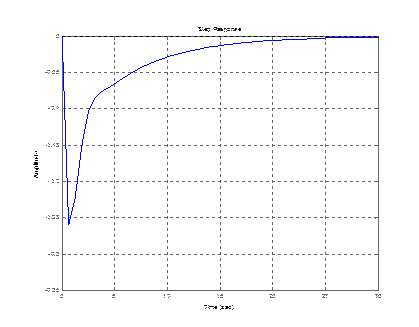
step (zam(1,1))                        step (zam(2,1))

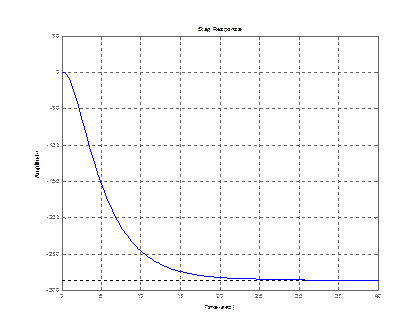
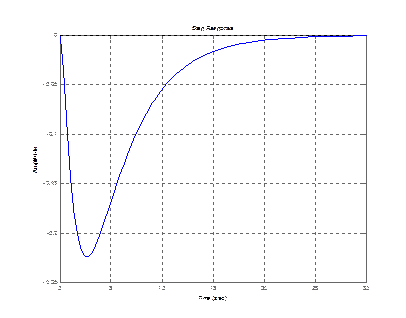
step (zam(3,1))

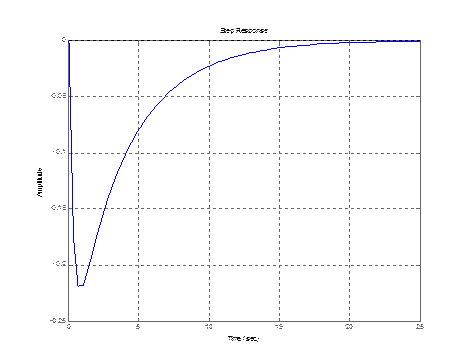
4) 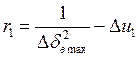, где , т. е

pzmap(zam)

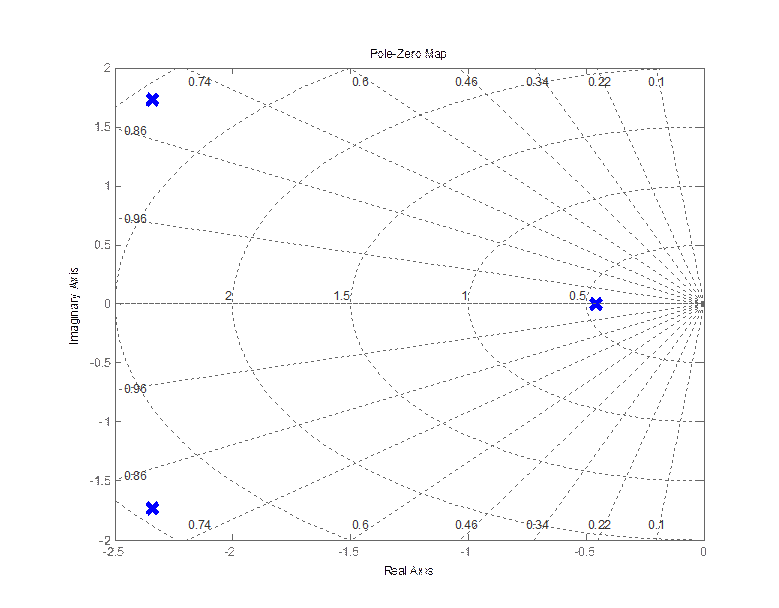
nyquist (zam(1,1))                     nyquist (zam(2,1))

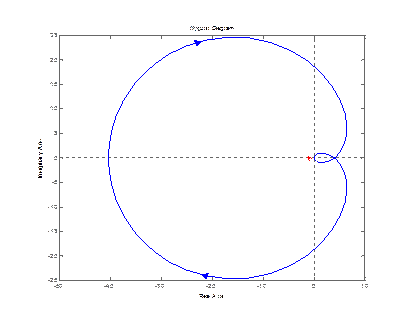
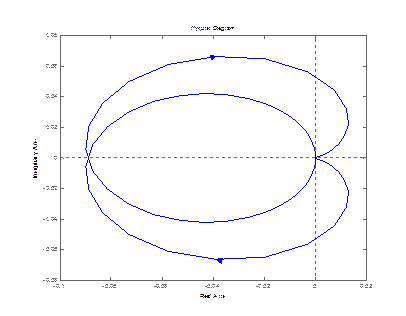
nyquist (zam(3,1))

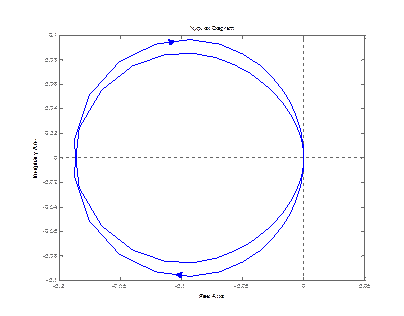
step (zam(1,1))                    step (zam(3,1))

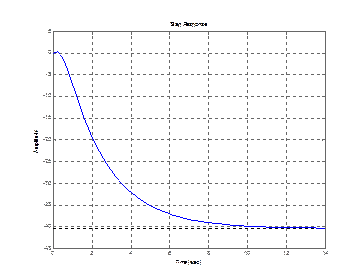
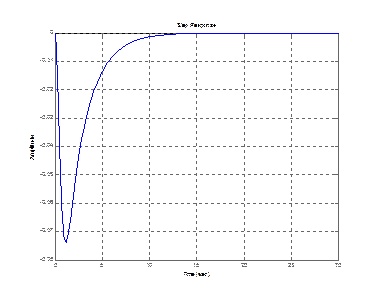
step (zam(3,1))

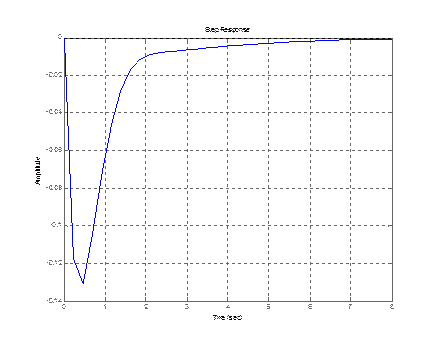
8. Вывод.

Можно проанализировать полученные данные, при варьировании коэффициентов матрицы Брайсона и сравнить их с изначальными результатами. Тогда получаем, что:

Для 1 случая:

При  ЛАФЧХ по всем переменным состояния существенно не изменяются. Исследование по годографу Найквиста показывает, что запасы устойчивости по переменным состояния углу тангажа и скороподъемности уменьшаются, а по переменным состояния углу атаки запас неустойчивости увеличивается, следовательно дальнейшее увеличение  ухудшит устойчивость по всем переменным состояния. Реакция на ступенчатое воздействие изменилась, уменьшилось время переходных процессов, возрастает колебательность при ступенчатом воздействии по всем параметрам, увеличивается амплитуда колебаний.

Для 2 случая:

При  ЛАФЧХ по всем переменным состояния существенно не изменяются. Исследование по годографу Найквиста показывает, что запасы устойчивости по переменным состояния углу тангажа и углу атаки уменьшаются, а по переменным состояния скороподъемности запас неустойчивости практически неизменен. Увеличилось время переходных процессов.

Для 3 случая:

При  ЛАФЧХ по всем переменным состояния существенно не изменяются. Исследование по годографу Найквиста показывает, что запасы устойчивости по переменным состояния углу тангажа и углу атаки уменьшаются