Кластерный анализ. Распределение n-объектов наблюдения в двухмерном пространстве, страница 2

 

59         363           268          129

113         263           229          100

Х=         70         313           193            90

94         412           257            84

37           81           298          119

Проведем нормирование данных по варианту: Zij=Xij/Xj, для этого предварительно следует рассчитать средние значения каждого из признаков:

X1=.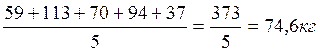

Аналогичным образом получаем, что Х2=286,4 кг; Х3=249 шт; Х4=104,4 кг, тогда Z11=59/74,6=0,79; Z12=363/286,4=1,27; Z21=113/74,6=1,51 и т.д.

Получаем матрицу нормированных данных:

 

0,79        1,27           1,08        1,24

1,51        0,92           0,92        0,96

Z=      0,94        1,09            0,78       0,86

1,26        1,44           1,03        0,8

0,5          0,28           1,2          1,14

Теперь надо найти расстояние между всеми парами стран, если выберем метрику L1-норма, то для первой пары Россия - США расстояние будет:

d12= I0,79-1,51I + I1,27-0,92I + I1,08-0,92I + I1,24-0,96I = 1,51;

для второй пары стран, Россия - Великобритания, расстояние равно:

d13= I0,79-0,94I + I1,27-1,09I + I1,08-0,78I + I1,24-0,86I = 1,01 и т.д.

Получим симметричную матрицу расстояний:

 

0         1,51        1,01         1,13          1,5

1,51     0             1,42         1,04          2,11

D0=    1,01     1,42        0              0,98          0,95

1,13     1,04        0,98         0               2,34

1,5       2,11        0,95         2,34          0

В кластерном анализе часто применяются три алгоритма кластеризации данных: «ближайшего соседа», «дальнего соседа» и «средней связи». Выберем алгоритм «дальнего соседа», тогда на первом шаге объединяются два ближайших объекта, по матрице D0 эти объекты Х3 и Х5 (Великобритания и Япония), для них dij - минимально, d3,5= 0,95, получим следующие кластеры:

Кластер	1	2	3	4
Объект	1	2	3,5	4

Теперь необходимо определить расстояние до кластера 3 всех других объектов (кроме 3,5), для первого объекта до кластера два не изменится d1,2=1,51; до кластера три будет выбрано из 1,01 и 1,5, d1,3=1,5; до кластера четыре вновь расстояние останется неизменным 1,13 и т.д. для всех объектов. После выделения первого кластера S3,5 исходная таблица расстояний (D0) сожмется и изменит свои характеристики:

 

0         1,51        1,5          1,13

1,51     0             2,11        1,04

D1=    1,5       2,11        0              0,98

1,13     1,04        2,34         0

На втором шаге можно объединить объекты 2 и 4 (США и Франция), так как для них расстояние минимально, d2,4=1,04; состав кластеров теперь уже будет:

Кластер	1	2	3
Объект	1	2,4	3,5

Определим расстояния между кластерами с учетом объединения новых объектов:

0         1,51        1,5

D2=    1,51     0             2,34

           1,5       2,34        0

0       2,34

На последнем шаге присоединим объект 1 к кластеру S3,5 и D3=   2,34   0

По результатам кластерного анализа построим дендограмму, при этом на оси Х будем откладывать номера кластеров, а по оси У - расстояние между кластерами:

 dij

2

1

1                   2                  3               4               5                Sij

Рис.3 Результаты иерархического кластерного анализа.

По данным рисунка целесообразно выделить следующие кластеры: S1 с объектами 3,5 (Великобритания, Япония); S2 с объектами2,4 (США, Япония) и S3 с одним объектом 1 (Россия), в общем можно заключить, что Россия по уровню потребления продуктов питания имела большее сходство с Великобританией и Японией, чем с США и Францией.