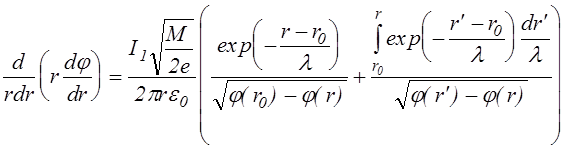Тлеющий разряд с полым катодом при малом разрядном токе, страница 4

   (3.2.1)

с граничными условиями

j(r₀)=0, j '(r₀)=0,                                                             (3.2.2)

где  I₁  - ток, протекающей в слое с единичной длиной в  продольном направлении.

Аналитическое решение  (3.2.1)  возможно лишь в  некоторых предельных случаях. При малых расстояниях  dr=r-r₀   от поверхности эмиттера, где выполняются условия

dr<<r₀ , dr<<l(3.2.3)

можно пренебречь  вторым членом в скобках в правой  части  (3.2.1),  а в первом члене положить  exp(-(r-r₀ )/ l)=1. Полагая также в левой части       

r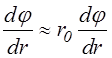                                                                        (3.2.4)

получим уравнение

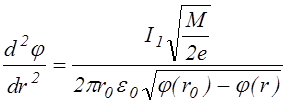,                                       (3.2.1¢)     решение которого

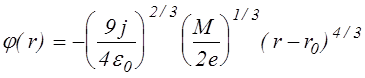,                          (3.2.5)

где  j = I₁/2pr₀ - плотность тока ионной эмиссии из плазмы,  соответствует бесcтолкновительному случаю в плоской геометрии.

При выполнении условия dr/l>>1 можно пренебречь первым членом в правой части  (3.2.1)  и разложить j(r') в  подинтегральном  выражении   в ряд в окрестности точки r

j(r')= j(r)+ j '(r)(r'-r).                                                     (3.2.6)

Учитывая также, что при больших  x

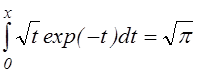,                                                    (3.2.7)

получим

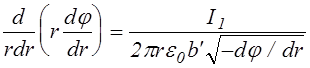                                   (3.2.8)

где

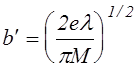.                                                                 (3.2.9)

Как видно из  (3.2.8), проведенная  процедура  соответствует принятию допущения, что средняя  скорость  ионов  определяется законом подвижности в сильных полях  v=b'.

Уравнение  (3.2.8)  имеет решение

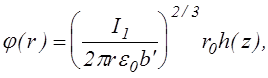                                             (3.2.10)

где      

h(z)=z²+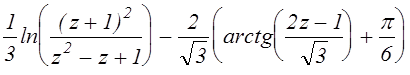,    (3.2.11)

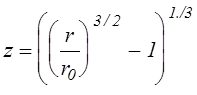.                                                        (3.2.12)

Переходя к рассмотрению общего случая введем безразмерные величины

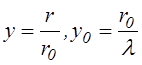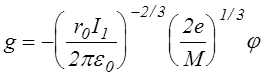,                     (3.2.13)

и запишем  (3.2.1)  в виде

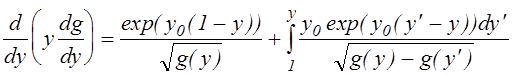     (3.2.14)

при граничных условиях

g(1) =0,  g'(1) =0.                                                   (3.2.15)

Уравнение  (3.2.14)  решалось численно  и  результаты  расчетов для различных параметров  y₀   приведены на рис. 3.2. При  y₀ = 0,  т.е. в бесcтолкновительном режиме,

g(y,y₀)=g₀(y)=(9yb²(y)/4)^2/3.                                          (3.2.16)

Функция g₀(y) изображена на рис.3.2 штриховой линией.

Возвращаясь к прежним переменным, получим связь между током, протекающим в слое, и распределением потенциала в виде

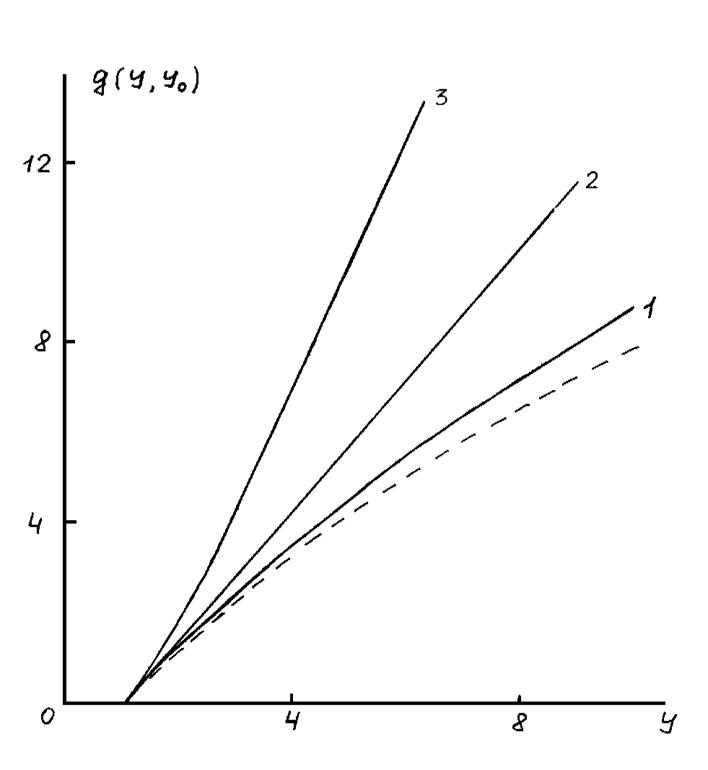
Рис 3.2. Зависимости g(y,y₀) для различных параметров y₀

1 - y₀=0.1, 2 - y₀ =1, 3 - y₀=10.

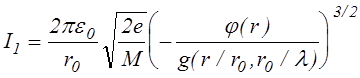                           (3.2.17)

Используя  (3.2.17), запишем выражение для первеанса

P=jU^-3/2,                                                                           (3.2.18)

характеризующего пропускную способность цилиндрического промежутка между плазмой и электродом с единичной площадью  на  поверхности плазменного эмиттера,                        

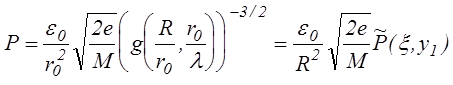             (3.2.19)

где                    

                                       (3.2.20)

При заданном  R  функции  , приведенные  на  рис.3.3 для различных параметров y₁, oпределяют вид  зависимости  удельной      пропускной способности промежутка   d_c=R-r₀   от  величины x. При y₁®0 , ®, где

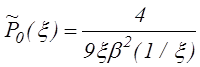                                                       (3.2.21)

есть удельная пропускная способность промежутка в бесcтолкновительном случае (cм. штриховую линию на рис.3.3). Как  видно из рисунка, в столкновительном режиме сохраняется  выявленный в параграфе 3.1. немонотонный характер зависимости P(x), который обуславливает неустойчивость системы плазма-слой при x<x_m, где x_m -  точка, в которой P(x) достигает  минимума.  Oднако положение этого минимума несколько смещается с изменением параметра y₁, т.е. с изменением давления

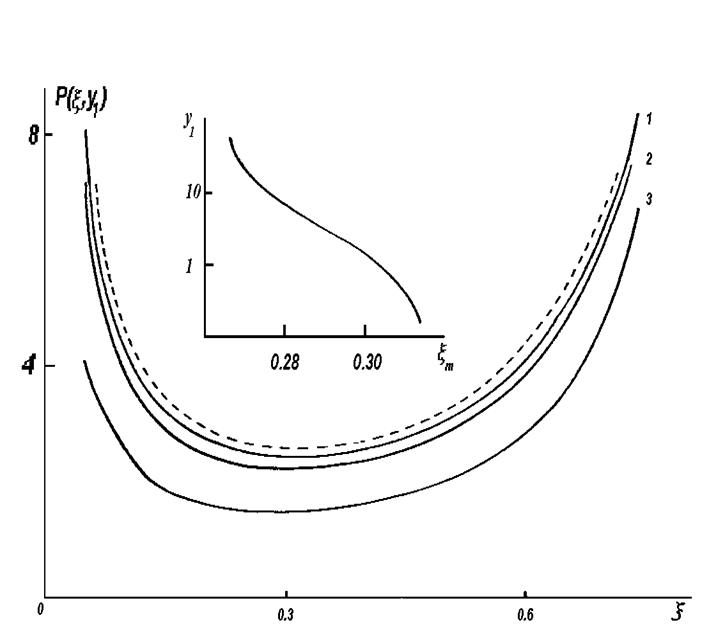
Рис. 3.3. Зависимости P(x,y₁) для различных параметров y₁

1 -  y₁ = 0.1, 2 - y₁ = 1, 3 - y₁ = 10.

газа. При y₁>>1, используя   (3.2.10), для   можно записать

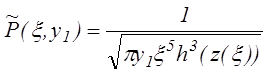                                         (3.2.22)

где  z(x)=(x^-3/2-1)^1/3.  Функция  (3.2.22)  имеет минимум в точке 0.263. Таким образом, x_m ® 0.263  c увеличением давления. С уменьшением давления  x_m  несколько возрастает и при  y₁®0, x_m ® 0.316.