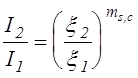Тлеющий разряд с полым катодом при малом разрядном токе, страница 3

                                                                   (3.1.6)

где m_c=1, m_s=2. Возможноcть практичеcкой реализации этих cоcтояний,  завиcящая от уcтойчивоcти границы плазмы к изменению величины x, влияет, в чаcтноcти на уcловия горения и  параметры  разряда c  полым катодом.

Рассмотрим вопрос об устойчивости границы плазменного образования с постоянной концентрацией  n  и радиусом  x   при  cлучайном малом возмущении dx. В результате расширения плазмы сокращается промежуток между ее границей и электродом, что привoдит к изменению его пропускной способности и  нарушению  необходимого  для выполнения соотношений  (3.1.4),
(3.1.5)  условия

j'(r₀) = 0.                                                                             (3.1.7)

Если x соответствует участку возрастания  f_c,s(x), то  возмущение dx  приведет к увеличению удельной  пропускной  способности промежутка и она станет  больше, чем  эмиссионная  способность плазмы. При этом на границе  плазма-слой  со  стороны  ионного слоя появится нескомпенсированное пространственным зарядом поле, вызывающее разделение зарядов на границе и  возврат плазмы в исходное состояние. Если же x находится на  участке убывания,  то случайное расширение плазмы приведет к тому, что  пропускная способность промежутка станет меньше, чем эмиссия из плазмы, и в нем появится избыточный ионный заряд. В результате на границе возникает поле, ускоряющее электроны плазмы в сторону внутренней поверхности полого электрода, что приведет к нарастанию возмущения.

Таким образом, устойчивое  существование в полости  системы плазма-слой возможно не при любых x, а  лишь  при выполнении в  сферической полости соотношения

x   >  0.45 ,                                                                           (3.1.8)

а  в  цилиндрической полости

x  >  0.31.                                                                             (3.1.9)

Из наличия у функций f_c,s(x) минимума (minf_c(x)=5.8,  minf_s(x)=12) с учетом  (3.1.4), (3.1.5)  следует вывод о том, что разность потенциалов между катодом и плазмой  с  известной концентрацией и температурой должна отвечать условию:

U  A_c,s n^2/3T_e^1/3R^4/3                                                      (3.1.10)

где A_s =2.15×10^-8   в сферической и A_c =8.79×10^-8   в цилиндрической геометриях. При увеличении разности потенциалов выше предела, определяемого  (3.1.10), будет происходить распад плазмы  в  полости, либо  разделение зарядов на входе в полость с формированием  двойного слоя. В последнем случае плазма внутри полости  приобретает потенциал, отличный от потенциала плазмы вне полости.

Преобразуя (3.1.10) можно получить оценку нижней границы для концентрации плазмы в разряде с полым катодом

n_cr  ~  A_c,s^3/2T_e^1/2R²U^3/2 .                                                (3.1.11)

Поскольку эмиссионная способность плазмы пропорциональна концентрации,  то полученное соотношение в свою очередь определяет минимальную возможную плотность тока в ионных и электронных источниках на основе разряда с полым катодом

3.2   Анализ устойчивости плазмы в цилиндрической геометрии в столкновительном режиме.

Учитывая, что во многих ситуациях,  возникающих  в газоразрядных структурах, реализуется столкновительный  режим,  предcтавляется целесообразным провести обобщение предложенной  модели на случай столкновительной системы плазма-слой. При  проведении анализа ограничимся характерным для  разрядов  низкого давления случаем сильных полей, когда  тепловая  энергия атомов мала по сравнению с энергией,  приобретаемой  ионом  на длине свободного пробега l. Рассмотрение  проведем только в цилиндрической геометрии.

В [91,92] рассматривались характеристики столкновительного ионного слоя в плоской и цилиндрической геометриях для случая сильных полей при использовании допущений, что основным процессом взаимодействия ионов с атомами является перезарядка, сечение которой не зависит от скорости иона, поле на  границе  плазма-слой  равно нулю. При этих допущениях  уравнение  Пуассона  для ионного слоя в цилиндрической геометрии имеет вид