Движение заряженных частиц в режиме частых столкновений, страница 2

(dE/dx) << E                                                                       (17)

то с хорошей точностью можно считать, что средняя энергия и вид энергетического спектра в некоторой точке являются функцией от локального значения Е/р. При выполнении противоположного условия спектр и энергия зависят от распределения потенциала в пространстве.

3. Диффузия электронов

Если плотность частиц неоднородна в пространстве, то возникает так называемый диффузионный поток, направленный из области с высокой концентрацией частиц в область с низкой концентрацией и стремящийся выровнять распределение концентрации в пространстве. По закону Фика

Г_диф  = - Ddn/dx                                                                          (18)

где D - коэффициент диффузии. Из анализа кинетического уравнения для D получено следующее выражение

          D = <v²/3n_эф>                                                                             (19)

Мы с вами получим его из других соображений. Пусть электроны распределены в пространстве по закону Больцмана

n = n₀exp(ej(х)/kT)                                                                     (20)

Использование з-на Больцмана справедливо при отсутствии тока. Значит диффузионный и дрейфовый потоки компенсируют друг друга

- m_еndj/dx = - Ddn/dx = - Dn(e/kT)dj/dx                                   (21)

Следовательно

D/m=kT/e                                                                                        (22)

Это так называемое соотношение Эйнштейна. Вспоминая, что средняя энергия частиц связана с температурой соотношением

          <e>=3kT/2                                                                              (23)

получим

D = 2m<e>/3e = 2 (e/mn_эф)(m/2)/3e = /3n_эф         (24)

4. Движение ионов в газе

Для ионов уравнение движения имеет следующий вид

Mdv/dt = eE - m<v(v)>                                                           (42)

При движении через газ состоящий из частиц другого сорта основным является поляризационное взаимодействие, транспортное сечение которого обратно пропорционально корню квадратному из энергии относительного движения, т.е. обратно пропорционально скорости. Тогда частота является постоянной и в стационаре (=0) получаем

v_д = 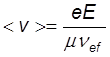                                                                          (43)

Похоже на то, что было для электронов но в знаменателе стоит не масса частицы, а приведенная масса. Соответственно подвижность ионов

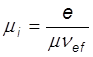                                                                               (44)

При движении в собственном газе основной процесс - перезарядка, сечение которой в первом приближении можно считать постоянным. Сделаем приближенную оценку подвижности для случая слабых электрических полях, когда скорость направленного движения много меньше хаотической скорости. Заменим среднее от произведения на произведение средних величин

<v(v)> ~ <v><(v)>.                                                        (45)

Величина <v> это и будет скорость дрейфа, а что касается частоты, то можно принять

n_эф = Ns_тр v_{отн.хаот} = N2s_пер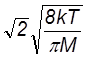                                            (46)

Учитывая также, что приведенная масса в этом случае равна  получаем для скорости дрейфа

v_д = 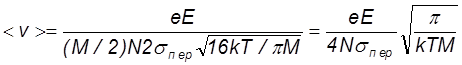         (47)

Поделив на Е получим оценку к-та подвижности.

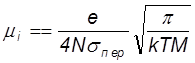                                                                    (48)

В результате более точных расчетов, чем выполненная оценка, для подвижности в слабых электрических полях получена следующая формула

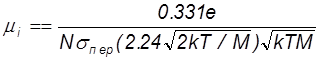,                                            (49)

отличающаяся от приведенной выше незначительно численным к-том, а также тем, что уточнено при какой скорости необходимо брать сечение перезарядки.

В сильных полях когда энергия, приобретаемая ионом на длине свободного пробега существенно выше тепловой энергии

eEv_d >> kT                                                                                   (50)

полученное соотношение перестает быть справедливым. Оценим величину m_i  в этом случае. Пусть в электрическом поле Е движется поток ионов j. Тогда для концентрации в некоторой точке можно записать

n = j/<v>                                                                                   (51)

C другой стороны для n можно записать следующее соотношение

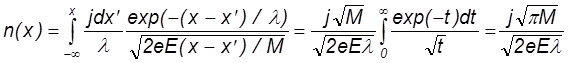   (52)

Сравнивая записанные выражения получим

<v>=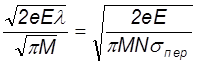                                                            (53)

Поделив на Е получим

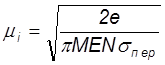                                                            (54)

Результаты более точных расчетов, учитывающих наличие слабой зависимости сечения перезарядки от скорости приводят к аналогичному выражению, но при этом уточняется при каком значении скорости надо брать величину сечения перезарядки

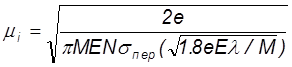                                 (55)

Итак в случае слабых электрических полей подвижность не зависит от Е, а в сильных полях обратно пропорциональна . Соответственно, в первом случае v ~ E, во втором  v ~ . Результаты экспериментов подтверждают наличие двух характерных участков на зависимости v(Е).

Что касается средней энергии ионов то в слабых полях она практически совпадает с тепловой энергией атомов, а в сильных      

<e> = eEl/2                                                                  (56)

Вопросы

1.  Получить выражение для коэффициента подвижности электрона.

2.  Чем определяется проводимость электронного газа?

3.  Какую энергию приобретает электрон в электрическом поле?

4.  Получить выражение для коэффициента диффузии электронов?

5.  Оценить подвижность ионов в слабых электрических полях

6.  Оценить подвижность ионов в сильных электрических полях

7.  Найти ВАХ газового промежутка с термокатодом при слабой эмиссии

8.  Найти ВАХ газового промежутка с термокатодом при сильной эмиссии