Движение заряженных частиц в режиме частых столкновений

Движение заряженных частиц в режиме частых столкновений.

В ионных и электронных источниках чаще всего реализуется режим прокачки плазмообразующего газа через газоразрядную систему. Если отбор частиц осуществляется через узкое отверстие, то в этом случае возможно возникновение значительного перепада давления между газоразрядной и ускоряющей системами. Тогда движение заряженных частиц в этих системах происходит в различных режимах. Если в ускоряющем промежутке практически всегда должно быть обеспечено выполнение условия l>>d, где d – длина промежутка, то в газоразрядной системе возможно выполнение обратного условия l<<L, где L – характерный размер газоразрядной камеры. В этом случае движение заряженных частиц к стенкам камеры (рекомбинация в объеме остается весьма маловероятным процессом) происходит в режиме.

1. Подвижность электрона

Рассмотрим задачу о движении электронов через газ в постоянном электрическом поле. Будем считать, что электроны заполняют все пространство и их концентрация постоянна. Тогда можно воспользоваться гидродинамическим уравнением движения

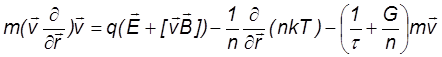
которое после соответствующих упрощений примет вид

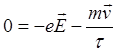
и для средней скорости  получаем

.

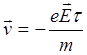Полученное выражение дает нам скорость дрейфа электрона через газ в электрическом поле. Именно скорость дрейфа, который, конечно, происходит на фоне достаточно сложного теплового движения. Чтобы подчеркнуть это обстоятельство у скорости часто ставят соответствующий индекс

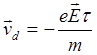
Казалось бы задача решена, но остаются некоторые сомнения по поводу того, чему же равно в данном случае время взаимодействия. Чтобы решить эту проблему воспользуемся следующими соображениями. На предыдущих лекциях мы выяснили, что воздействие атомов на движущийся электрон может быть представлено как действие силы трения mvn_эф. Таким образом закон Ньютона для движения электрона в электрическом поле через газовый промежуток можно записать как

                                                 (1)

В первый момент после включения поля или после возникновения электрона присходит его разгон электрическим полем но постепенно по мере увеличения направленной скорости возрастает и сила трения и при некоторой скорости, а именно при

                                                                       (2)

наступит стационарное состояние. Сравнивая полученные выражения делаем вывод, что в данном случае t=1/n_эф , т.е. под величиной тау надо понимать эффективное время между электрон – атомными столкновениями.

Коэффициент пропорциональности между v_d и Е называется подвижностью и обозначается символом m_е

v_d = m_еЕ                                                                                   (3)

Нетрудно видеть, что

m_е = е/mn_эф                                                                            (4)

Формулы очень простые и удобные, но пользоваться ими нужно достаточно осторожно, так как n_эф вообще говоря зависит от скорости, причем не от направленной скорости а от скорости относительного движения частиц, которая в большей степени определяется хаотической, а не направленной скоростью электронов. Поскольку сечение, а значит и частота меняются с энергией или со скоростью, то, соответственно, и скорость дрейфа, и это подтверждается результатами экспериментов, растет с увеличением Е не по линейному закону, а более сложным образом.

Кроме того результаты экспериментов подтверждают один интересный вывод, который следует и из нашей простой формулы и из точного решения кинетического уравнения. Это то, что при одновременном одинаковом изменении напряженности электрического поля и давления газа р скорость дрейфа не меняется. Действительно, поскольку n_эф ~  = р/kТ, то при заданном Т скорость

v ~ E/N ~ E/p                                                    (5)

и должна сохраняться при постоянном Е/р и меняться с изменением Е/р. Когда имеют место такого рода зависимости, где некоторая величина является функцией от некоторой комбинации других величин (необязательно Е/р), то говорят, что выполняется закон подобия. В дальнейшем мы познакомимся и с другими законами подобия.

Используя полученное выражение получим формулу для проводимости электронного газа. Проводимость это коэффициент пропорциональности между плотностью тока и напряженностью поля

j = сE                                                           (6)

C другой стороны

j = en_еv_д = enm_еE                                          (7)

Сравнивая выражения получаем

          с = en_еm_е = e²n_е/mn_эф (8)

Проводимость растет с увеличением концентрации электронов и с уменьшением частоты столкновений, т.е. с уменьшением давления.

2. Энергия электрона в электрическом поле

Уравнение баланса энергии выглядит следующим образом

de/dt = eEv_д - (2m/M)en_эф                                               (9)

Выход на стационар происходит при

e =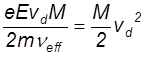                                                (10)

Это средняя энергия хаотического движения. Средняя скорость хаотического движения

v_х = 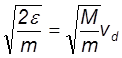                                                    (11)

значительно превышает скорость дрейфа.

Величину

n= 2mn_эф/M                                                            (12)

называют частотой потерь энергии и также вводят характерное время релаксации по энергии

                                                                      (13)

Если поле является переменным, но меняется достаточно медленно,

(dE/dt) << E                                                             (14)

то средняя энергия электронов и энергетический спектр успевают отслеживать изменение поля, в противном случае энергия электронов зависит от предистории, а не от значения Е в данный момент времени.

За время релаксации электроны успевают продрейфовать на расстояние

                                                                        (16)

Эту величину называют длиной установления или длиной релаксации энергии. Если поле меняется в пространстве но незначительно, так что