 |
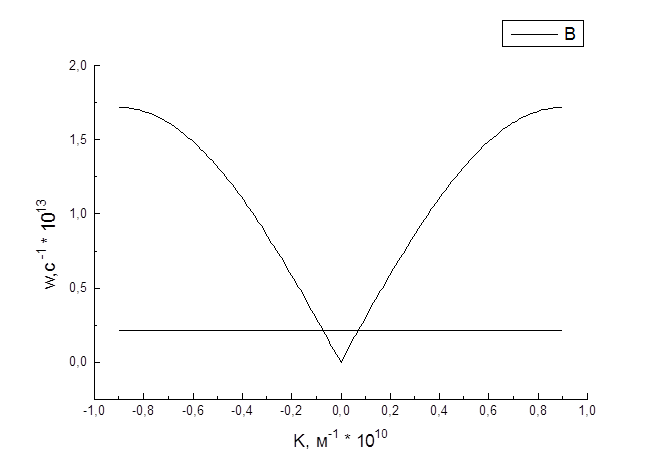
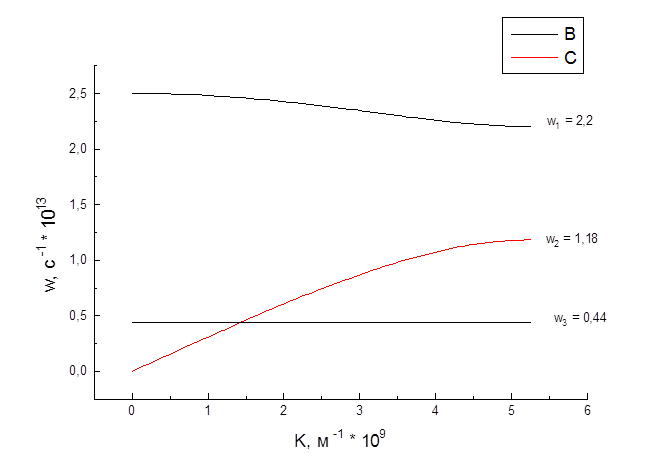
3) Рассчитала дисперсионную зависимость колебаний w1,2(k) для двухатомного кристалла LiF (Таблица 2 Приложения). Зафиксировав силовую постоянную и массу дефекта вольфрама W, рассчитала частоту локальных колебаний wлок =0,44×1012 с-1 и определила тип локального колебания как резонансные дефектные колебания для направления [100]. Из графика определила значения w1=2,2×1012 с-1 , w2=1,18×1012 с-1.
 |
2) Зафиксировав силовую постоянную и меняя массу дефекта (вольфрама W), построила зависимость локальной частоты от массы изотопической примеси в одноатомном кристалле Ni с ГЦК структурой.
Таблица с расчётами для построения графика:
|
Мдеф,кг×10-26 |
wлок , с-1×1012 |
|
81,468 |
7,954 |
|
85,994 |
7,473 |
|
90,52 |
7,048 |
|
95,046 |
6,669 |
|
99,572 |
6,329 |
зависимость локальной частоты от массы изотопической примеси в одноатомном кристалле Ni с ГЦК структурой, здесь wmax=2,943×1012 с-1
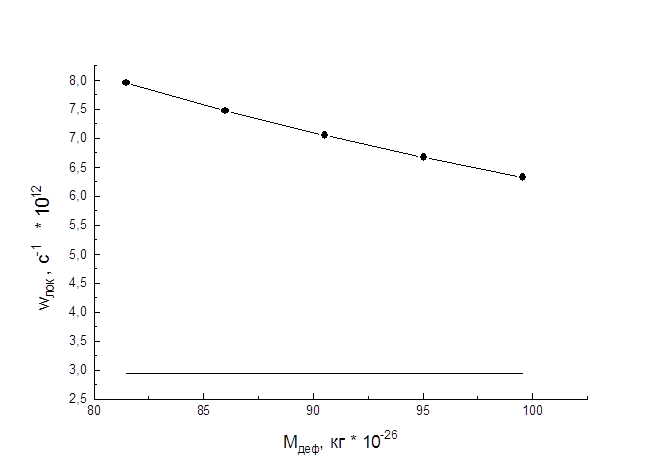 |
Цель работы: Получить эмиссионное изображение кристалла вольфрама и провести индексацию граней.
В ходе работы с помощью сфотографированного полевого электронного изображения кристалла вольфрама путём наложения на него стереографической проекции кристалла и сетки Вульфа идентифицировала грани кристалла (соответствующие тёмным областям на фотографии) и провела их индексацию: это плоскости [010], [121], [112], [001].
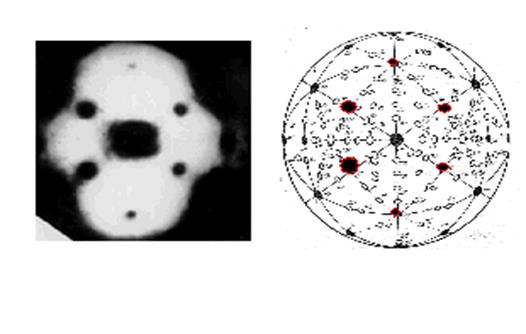 |
Решающее влияние на электронную эмиссию оказывает работа выхода электронов с различных участков кристалла. Кристаллографические грани с большей плотностью поверхностных атомов имеют большую работу выхода, этим объясняется то, что на изображении W- кристалла плоскость [112] выглядит тёмной. Соответственно, грань с меньшей плотностью поверхностных атомов имеет меньшую работу выхода и поэтому плоскость [111] выглядит светлой.
ЦЕЛЬ РАБОТЫ: Оценить степень вакуума в полевом эмиссионном микроскопе, используя явление полевой эмиссии.
Получив эмиссионное изображение, фиксируем напряжение и ток эмиссии, далее снимаем напряжение и даем выдержку по времени – 3 мин, после чего устанавливаем фиксированное напряжение и смотрим каков ток эмиссии.
|
U, кВ |
I,мА |
|
6,2 |
0,8 |
|
6,2 |
1,2 |
Если поверхность атомно-чистая, то ток будет такой же, как и в первом опыте, если произошла адсорбция, - ток изменится. Установив время, за которое изменился ток, по формуле (33) найдем давление в приборе.
Время полного покрытия поверхности газом τпокр. 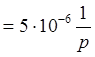 (33). Отсюда p=5×10-6/ τпокр= 5×10-6/180с=2,8×10-8 Тор.
(33). Отсюда p=5×10-6/ τпокр= 5×10-6/180с=2,8×10-8 Тор.
Цель работы: Знакомство с устройством и принципом действия автоэмиссионного микроскопа. Оценка увеличения.
Для острия радиуса r из металла с работой выхода j зависимость
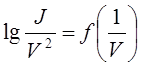 (11)
(11)
представляет прямую линию, т.к. логарифм силы тока, отнесенный к квадрату напряжения, линейно связан с обратным напряжением. Тогда
J= 10(A/V + 2lgV + B)
Средняя работа выхода вольфрама φ=4,5 эВ и в приближении Дрихслера-Хенкеля радиус острия эмиттера вычисляется по формуле
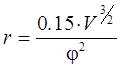 ,
(26)
,
(26)
где r
в ![]() , φ в эВ, V
- напряжение в вольтах, необходимое для получения тока 10 мкА (10-5А).
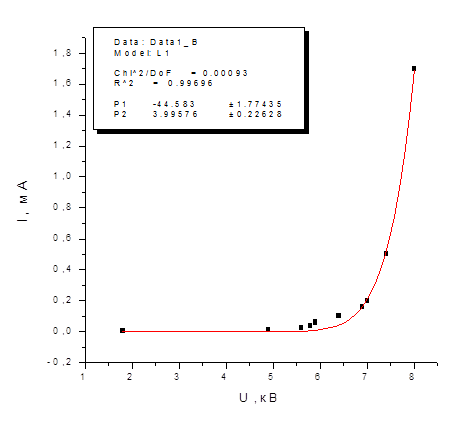
Таблица снятых экспериментально значений напряжения U и
тока I для построения ВАХ.
, φ в эВ, V
- напряжение в вольтах, необходимое для получения тока 10 мкА (10-5А).
Таблица снятых экспериментально значений напряжения U и
тока I для построения ВАХ.
|
U, кВ |
I, мА |
|
1,8 |
0,007 |
|
4,9 |
0,012 |
|
5,6 |
0,024 |
|
5,8 |
0,036 |
|
5,9 |
0,06 |
|
6,4 |
0,1 |
|
6,9 |
0,16 |
|
7,0 |
0,2 |
|
7,4 |
0,5 |
|
8,0 |
1,7 |
По графику нашли V= 4,9кВ при эмиссионном токе I= 0,01мА.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.