Помимо чистых металлов в качестве проводников широко применяют металлические сплавы со структурой не упорядоченного твёрдого раствора. Некоторые металлы могут смешиваться в любых пропорциях (образовывать непрерывный ряд твёрдых растворов), взаимная растворимость других металлов ограничена. Статистическое распределение атомов разного сорта по узлам кристаллической решетки вызывает значительные флуктуации периодического потенциала в кристалле, что приводит к росту рассеяния электронов. Удельное сопротивление сплава также скалдывается из рассеяния на фононах и примесях
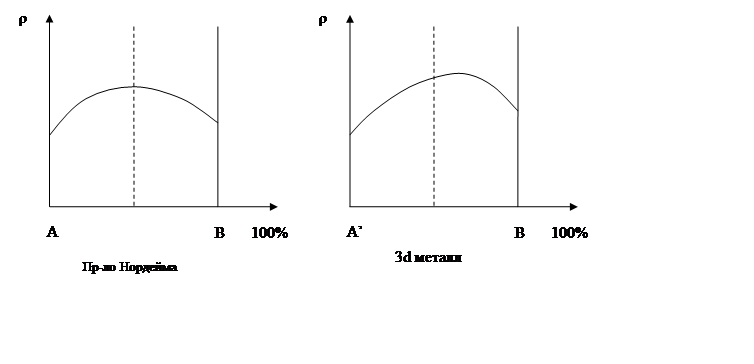
ρсплава = ρост + ρт , но ρост >> ρт из-за дефектности и ρост = ρдеф. Для многих двухкомпонентных сплавов выполняется закон Нордгейма:
ρост = С∙Xа Xв = С∙Xв∙(1 - Xв), где Xа, Xв – доля компонента в сплаве. Закон хорошо описывает непрерывные твёрдые растворы при отсутствие фазовых переходов в системе, когда компоненты не являются редкоземельными или переходными металлами. Для металлов переходных групп (3 d элементы) при высокой концентрации зависимость ρ существенно несимметрична, т.к. часть валентных электронов в сплаве из 3d металлов переходит из электронного газа на не полностью заполненную 3d оболочку.
В общем случае для температурного коэффициента aρ сплава можно написать следующее выражение
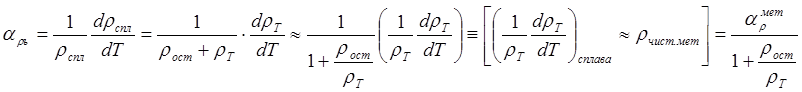
При ![]() >>
>>![]() ,
, ![]() <<
<<![]() . На
этом основывается получение термостабильных проводящих материалов. В некоторых
случаях r(Т) подчиняется
более сложной зависимости и
. На
этом основывается получение термостабильных проводящих материалов. В некоторых
случаях r(Т) подчиняется
более сложной зависимости и ![]() может быть равным нулю
или отрицательным.
может быть равным нулю
или отрицательным.
Некоторые сплавы нельзя рассматривать как классические металлы. В них при высоких температурах понижение подвижности ведущее к увеличению удельного сопротивления компенсирует высокая концентрация электронов. Также некоторые сплавы ниже температуры называемой температурой Курнакова из неупорядоченных структур превращаются в структурированные с дальним порядком, при этом удельное сопротивление уменьшается вследствие восстановления периодичности решётки.
Если компоненты не обладают взаимной растворимостью - образуется гетерогенный сплав, его r увеличивается пропорционально r металла с наибольшим удельным сопротивлением (линейная зависимость от концентрации), так как
![]() , где
, где ![]() - сопротивление фаз
- сопротивление фаз
Возможны отклонения от этого правила, обусловленное различием размеров частиц, их формой и распределением в материале. Для матричной основы с вкраплением частиц другой фазы:
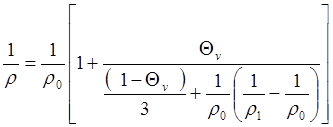 , где
, где ![]() - сопротивление матрицы,
- сопротивление матрицы, ![]() - сопротивление включений,
- сопротивление включений, ![]() - объёмная доля включений.
- объёмная доля включений.
На высоких частотах плотность электрического тока максимальна у поверхности проводника и убывает при удалении от нее вглубь образца.
Магнитный поток Ф,
созданный током I, определяется
выражением Ф=L∙I,
где L-индуктивность
материала. При его изменении возникает ЭДС самоиндукции ![]() ,
пропорциональная скорости изменения тока
,
пропорциональная скорости изменения тока
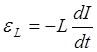
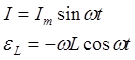
Данная ЭДС направлена
противоположно току и компенсирует его изменение. Действие ![]() максимально в центре проводника и
минимально на поверхности и для плотности тока выполняется:
максимально в центре проводника и
минимально на поверхности и для плотности тока выполняется:
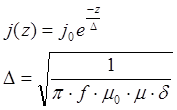 , где
, где ![]() характеризует глубину проникновения
электрического поля в проводник. Ток через проводник
характеризует глубину проникновения
электрического поля в проводник. Ток через проводник
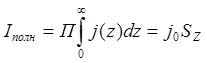 , где П- периметр сечения проводника,
, где П- периметр сечения проводника, ![]() - эквивалентная площадь сечения. При
высоких частотах j(z)=0 везде кроме слоя
- эквивалентная площадь сечения. При
высоких частотах j(z)=0 везде кроме слоя ![]() и сопротивление проводника увеличивается.
Для характеристики скин-эффекта вводится коэффициент увеличения сопротивления
проводника
и сопротивление проводника увеличивается.
Для характеристики скин-эффекта вводится коэффициент увеличения сопротивления
проводника
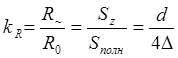
Проводящие металлические пленки как правило получают конденсацией молекулярных пучков в вакууме. В зависимости от условий конденсации они могут обладать различной структурой, от аморфной до монокристаллической, что изменяет их удельное сопротивление. На величину удельного сопротивления влияют также поверхностные процессы.
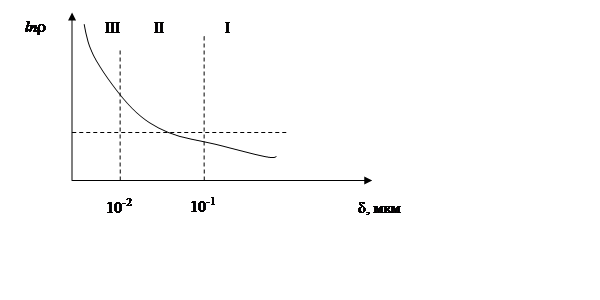
Изменение ρ в процессе конденсации происходит в несколько этапов (см. рисунок). На участке I толщина пленки δ » 0,1мкм, здесь наблюдается непрерывное покрытие поверхности, ρ»ρ массивного образца. На участке II c δ » 0¸10-2мкм сопротивление пленки значительно выше, чем в массивном образце за счёт высокой концентрации дефектов, как собственных, так и примесных, образовавшихся в момент выращивания. Здесь происходит слияние отдельных островков и образование проводящих цепочек и каналов. Участок III имеет островковую структуру
Поверхностные эффекты заключаются в том, что длина свободного пробега вдоль нормали к поверхности может быть ограничена размерами пленки. Это явление становится существенным при толщине ~ 200¸300Å. Для удельного сопротивления такой пленки можно написать выражение
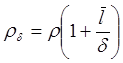 , где
, где ![]() -
средняя длина свободного побега , δ –толщина плёнки, ρ-удельное сопротивление
массивного образца. Для сравнительной оценки поводящих свойств тонких плёнок
используют величину “сопротивление квадрата”
-
средняя длина свободного побега , δ –толщина плёнки, ρ-удельное сопротивление
массивного образца. Для сравнительной оценки поводящих свойств тонких плёнок
используют величину “сопротивление квадрата”
R□![]()
Сопротивление тонкоплёночного резистора с шириной d0 и длиной l0 в направление прохождения тока, определяется как
R=R□![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.