Генерация, распространение и фокусировка лазерного излучения

Генерация распространение и фокусировка  лазерного излучения.

Рассмотренные в прошлых лекциях процессы усиления электромагнитного излучения и свойства резонатора позволяют нам понять как возникает генерация лазерного излучения .

Условия возникновения генерации достаточно очевидны. Усиление излучения за два прохода по активной среде, т.е., проход от полупрозрачного зеркала к глухому и обратно , равно потерям энергии в резонаторе, в том числе и энергия лазерного излучения.

Если пренебречь всеми потерями кроме потери на вывод излучения , то условия генерации можно записать так

I₀-интенсивность излучения падающего на полупрозрачное зеркало, I₀R-часть энергии, отразившаяся от полупрозрачного зеркала и ушедшая обратно в резонатор.

Далее, после усиления за два прохода в резонаторе (до глухого зеркала и обратно) она усилится и станет равной

Очевидно, что эта интенсивность должна оказаться равной исходной (I₀) .

В этом случае возникает генерация лазерного излучения с интенсивностью равной

I₀(1-R), т.е.,с той интенсивностью которая прошла через полупрозрачное зеркало.

В квантовой электронике принята другая форма записи условия генерации.

Где

Усиление за 1 проход. Это условие полностью эквивалентно записанному ранее.

Если RK²<1, то усиление не компенсирует потери и генерация не происходит.

Возникает вопрос , что будет если RK²>1. В этом случае , казалось бы начальная интенсивность излучение падающее на полупрозрачное зеркало, обусловленное например, спонтанным излучением, усиливает за два прохода возрастет, как это видно из формулы

После следующих двух проходов она возрастет еще больше, и так до бесконечности.

Однако такого не происходит из-за эффекта насыщения. Из прошлых лекций мы знаем что коэффициент усиления g падает с ростом интенсивности излучения в резонаторе.

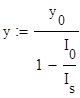
То есть при возрастании интенсивности I₀, коэффициент усиления в резонаторе будет падать пока не получится точного равенства о котором мы говорили в начале лекции.

Очевидно, что чем больше «запас» по усилению, тем больше интенсивность излучения лазера и больше его КПД. Однако, при росте интенсивности возрастают потери на поглощения на зеркалах резонатора, которыми мы пренебрегли в начале. По этому при расчете оптимальных параметров резонатора (Он достаточно сложен) учитываются и минимизируются все возможные потери.

В случае когда  «запас» по усилению не большой генерация возникает в одномодовом режиме, только для моды имеющей максимальный коэффициент усиления.

В результате получается слабое но качественное излучение.

Если запас по усилению достаточно большой, то условие генерации выполняется для нескольких мод и происходит многомодовая генерация. Излучение получается более мощным но менее качественным. Поэтому, при проектировании лазера добиваются компромисса между мощностью и качеством излучения .

Условие генерации для неустойчивого резонатора можно записать по аналогии с устойчивым, только вместо R надо подставить величину равную отношению площадей апертур меньшего зеркала к большему

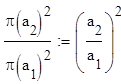
То есть условие возникновения генерации запишется следующим образом

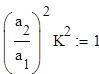
При распространении лазерного луча на большие расстояния неизбежно происходит увеличение его апертуры. Это явление называется расходимостью лазерного излучения. Чаще всего расходимость вызвана изначальной небольшой непараллельностью лазерного луча и называется геометрической расходимостью. Точный расчет угла геометрической расходимости возможен только после расчета конфигурации электромагнитного поля в резонаторе. Оценочную формулу для этого угла q можно получить исходя из следующего рисунка:

Очевидно, что максимальное оклонение лазерного луча от оптической оси резонатора определяется следующим условием. Луч должен совершить два прохода вдоль резонатора и не выйти при этом за пределы его апертуры. Следовательно, угол q_г определяется следующей формулой:

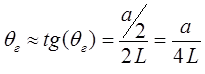
где: a – апертура луча на выходе, L – длина резонатора.

Однако даже идеально параллельный лазерный луч будет неизбежно расходиться вследствие дифракции. Угол дифракционной расходимости можно оценить по формуле:

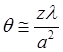                                                         (2.1.5)

где z путь пройденный лазерным лучем, l- длина волны.

Распределение электромагнитного поля при z®¥ называется распределение в дальней зоне. Оно же справедливо и в фокусном пятне, поскольку при фокусировке оптический путь луча обращается в бесконечность. Для этого полученное распределение поля на зеркалах резонатора снова подставляется в интеграл Френеля Кирхгофа, но записанный уже в другом виде, где учтено стремление z к ¥. По форме он схож с преобразованием Фурье:

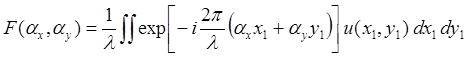                           (2.1.6)

В результате вычисляется распределение интенсивности по углу расходимости. Геометрическое распределение интенсивности в фокальном пятне I(x₂,y₂) вычисляется с помощью следующих соотношений:

                                                       (2.1.7)

где f – фокусное расстояние линзы.

Лучше всего фокусируется гауссова мода устойчивого резонатора (TEM₀₀), ее вид описывается функцией Гаусса, которая остается при m и n = 0 в формуле (2.1.3):

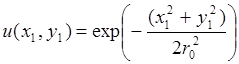                                           (2.1.8)

Эта мода является своеобразным “эталоном” фокусировки, поскольку сохраняет при фокусировки свой вид (функция Гаусса не меняется при преобразовании Фурье). Хуже фокусируются моды более высокого порядка.

В случае неустойчивого резонатора когда излучение выводится в форме кольца распределение поля в фокусном пятне будет иметь вид гауссоиды в центре окруженной серией колец. Поперечное сечение  этой функции представлено на рисунке 1

(Рисунок 1)

Видно что чем тоньше кольцо тем меньше центральная гауссоида и больше окружающие ее кольца. Это означает более плохое фокусное пятно с точки обработки фокусных материалов.