Емкостные накопители энергии. Общие сведения о емкостных накопителях энергии (ГИН, ГИТ, ФЛ), страница 2

В особом случае, когда активным сопротивлением контура можно пренебречь (R=0), решение для случая (а) упрощается

(3.9)

где 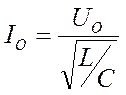   - максимальный ток; период колебания в такой цепи равен

(3.10)

Выразим период и ток через энергию, запасенную в конденсаторе

(3.11)

Получим:

	(3.12)
	(3.13)

Начальная скорость нарастания тока максимальна и составляет (для всех случаев а,б,в)

(3.14)

Максимальный ток I_m = I_O, и время его нарастания О,25Т связаны соотношением: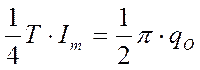          

При рассмотрении вопроса генерации больших импульсных токов одной из наиболее важных количественных характеристик цепи является значение тока в первом максимуме (I_m) и время его достижения (t_m). Эти значения легко получаются максимализацией выписанных ранее решений:

а) 0 ≤ γ < 1 (колебательный режим)

	(3.15)

б) 1 < γ < ∞ (апериодический режим)

	(3.16)

в) γ = 1 (критический режим)

	(3.17)

3.2.3. Энергетические характеристики RLC-контура.

Энергия элементов цепи в момент первого максимума тока равна (t = t_m):

W_C = W_R,m + W_L,m + W_C,m – полная энергия

- энергия, рассеянная в R	(3.18)
- энергия, запасенная в индуктивности	(3.19)
- энергия, оставшаяся в конденсаторе	(3.20)

Наибольший интерес представляют (3.18), (3.19), которые отражают эффективность вывода энергии из С в R или L. Оценим эффективность вывода в активную и индуктивную нагрузки.

Используя уравнения (3.12) и (3.19), представим эффективность передачи энергии от батареи конденсаторов (W_O) к катушке (W_L) в момент максимума тока t_m:

(3.21)

где L_O + L_H = L – полная индуктивность контура.

Из последнего выражения следует, что для увеличения эффективности передачи энергии в нагрузку необходимо стремиться к уменьшению (L_O/L_H) и R = R_O + R_H. На практике эффективность может достигать 90 %.

При работе ГИТ на активную нагрузку важным вопросом является получение в ней максимальной мощности P_max = I_m²·R. Используя для I_m выражение (3.15), для I_O – (3.12) и записывая 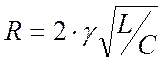, получаем:

(3.22)

где A = 2U_OI_O.

            Задача отыскания оптимального γ для получения максимально возможной мощности при заданных W_O, L и C сводится к максимализации выражения 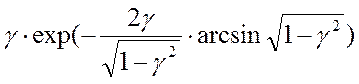 по γ. Опуская промежуточные выкладки, запишем

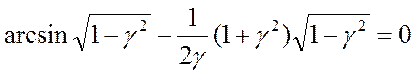
Решение уравнения дает γ^опт = 0,55 или:

	(3.23)
	(3.24)
	(3.25)

При этом средняя максимальная скорость нарастания мощности равна

(3.26)