Аналитическая функция взаимной корреляции детерминированных процессов, страница 2

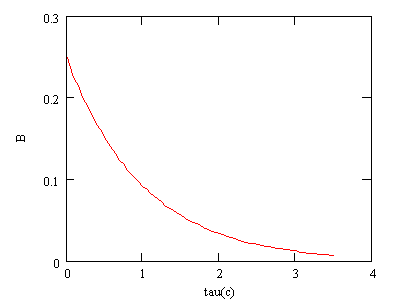
Рис. 3 График взаимокорреляционной функции если сигнал  на время τ.

Если τ <0 т.е. сигнал  опережает на время τ сигнал . Взаимокорреляционной функции равна 0 и рассматривать такой случай нет смысла.

Задача № 2.

По энергетическому спектру стационарного случайного процесса, действующего на входе линейной системы c импульсной характеристикой . Найти и построить функцию корреляции и энергетический спектр процесса на выходе.

Дано:

 - спектр мощности входного сигнала;

 - импульсная характеристика линейной цепи:

Решение:

Коэффициент передачи линейной цепи определяется по формуле (2):

                       (2)

Функцию корреляции для случайного процесса определим согласно формуле (3):

               (3)

Спектр мощности выходного сигнала определим согласно формуле (4):

                               (4)

Определим частотный коэффициент передачи линейной цепи при известной импульсной характеристике. Для этих целей используем формулу (2) (интеграл берется с использованием гамма - функции):

;

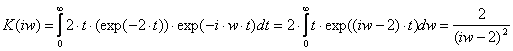Определим функцию корреляции, для случайного процесса, для этих целей используем формулу (3) (интеграл по замкнутому контуру, аналитическая функция имеет изолированную особую точку – полюс, вычисление интеграла сводится к определению вычетов по полюсам):

;

;

Определим полюс: в верхней полуоси функция имеет единственную особую точку  - это полюс 3 – го порядка: