Потери энергии, пробеги ионов в твёрдых телах. Ядерное торможение (упругое взаимодействие с атомами мишени), страница 2

Обсудим наиболее важные моменты торможения и распределения ионов, а также распределения радиационных дефектов.

Как мы уже говорили, при относительно низких энергиях, наиболее существенную роль играют два основных эффекта: 1) упругое соударение с ядрами и 2) неупругое соударение с электронами.

Допущение о том, что оба процесса не зависимы друг от друга, позволяет записать следующее выражение для потерь на единицу пути:

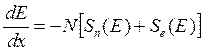.                                         (11.1)

Если величины S_n(E) и S_e(E) известны, то пробег может быть вычислен следующим образом:

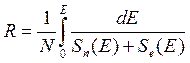,                                            (11.2)

где R – средняя общая длина пути частицы с начальной энергией E в аморфном теле.

11.1.1. Ядерное торможение (упругое взаимодействие с атомами мишени)

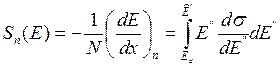,                          (11.3)

,                               (11.3a)

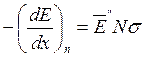                                          (11.4)

ds = 2πpdp – дифференциальное сечение dзаимодействия, p – прицельный параметр

E” – кинетическая энергия, передаваемая движущимися атомами атомам мишени.

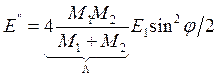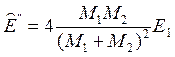               (),                    (11.5)

,       ,                                           (11.6)

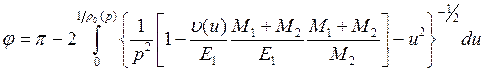.            (11.7)

В ЛШШ теории используется экранированный Кулоновский потенциал в виде 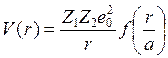                                                                                  ,                                    (11.8)

где 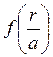- функция экранирования, - параметр экранирования (по порядку величины равный боровском радиусу ).

Линхард и Шарф использовали потенциал в степенной форме:

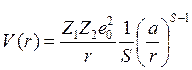,                               (11.9)

Простой аналитический вид зависимости получается из S=1 и 2. При S = 1 мы имеем кулоновский потенциал, при столкновение передаётся большое количество энергии, а при S = 2 мы имеем обратноквадратичный потенциал и при столкновении передаётся малое количество энергии. Наилучшее же совпадение получается в модели Томаса-Ферми. Это модификация той модели, что мы рассмотрели. Величина а  находится как решение дифференциального уравнения

.                                      (11.10)

Она определяется следующим выражением

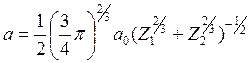,                    (11.11)

а₀ – радиус Бора (а₀ = 0,53Å)

С помощью этого потенциала Линхард, Шарф и Шиотт рассчитали дифференциальное сечение для ядерного торможения, введя безразмерные пробег, энергию и параметр рассеяния:

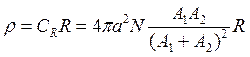                                 (11.12)

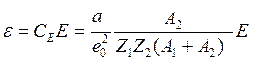,                                           (11.13)

 

,                                                        (11.14)

где (А₁ и А₂ – атомные массы иона и мишени). Они получили универсальное соотношение для сечения торможения S_n (или удельных потерь энергии). Это соотношение справедливо для всех комбинаций ион-мишень и в принятых единицах величина S_n безразмерна.

Таблица 11.1.

Значения энергий E₁,E₂,E₃ (см. Рис. 11.1) для различных комбинаций ион-мишень

мишень Ион	E1,кэВ			Е2, кэВ			Е3, кэВ
	Si	Ge	Sn	Si	Ge	Sn	Si	Ge	Sn
B	3	7	12	17	13	10	3·103
P	17	29	45	140	140	130	3·104
As	73	103	140	800	800	800	2·105
Sb	180	230	290	–	–	–	6·105
Bi	530	600	700	600	600	600	2·106

Для тяжелых ионов все энергии слабо зависят от сорта мишени.