Электронное торможение. Распределение пробегов

Лекция 12

12.1. Электронное торможение.

При высоких энергиях > 10⁷-10⁸ МэВ справедлива теория Бете-Блоха. Низкие энергии наиболее подробно рассмотрели Линхард и Винтер. Они предположили, что электроны формируют газ свободных электронов и показали, что электронное торможение (его сечение S_e(E)) пропорционально скорости ионов или, иначе, корню квадратному из их энергии:

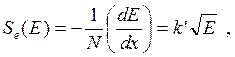                                                                                                                                            (12.1)

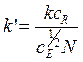,                                                                                                                                            (12.1)

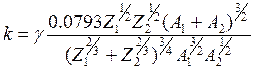,                                                                                                                                            (12.1)

где g - безразмерная константа того же порядка, что и , и- коэффициенты пропорциональности, значения C_E и С_R определяются соотношениями (11.12) и (11.13). В нормированном представлении

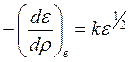.                                                                                                                                            (12.1)

Для большинства комбинаций констант мишень k=0.1¸0.25. Последнее соотношение справедливо для скоростей . При более высоких скоростях работает теория Бете-Блоха.

Сечение ядерного и электронного торможения, вычисленные с помощью ЛШШ теории, представлены на рис. 12.1.

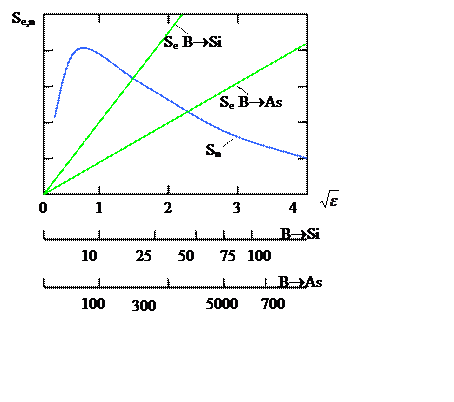
Нормализованные сечения торможения S_e и S_n

для B⁺ и As⁺, имплантируемых в кремний

Рис. 12.1.

Несколько иная теория торможения была рассмотрена Фирсовым для электронного торможения. Он предположил, что движущиеся атомы и атомы матрицы во время столкновения формируют квазимолекулы. Это объясняет причину осцилляции (немонотонности) зависимости S_e от Z₁.

12.2. Распределение пробегов.

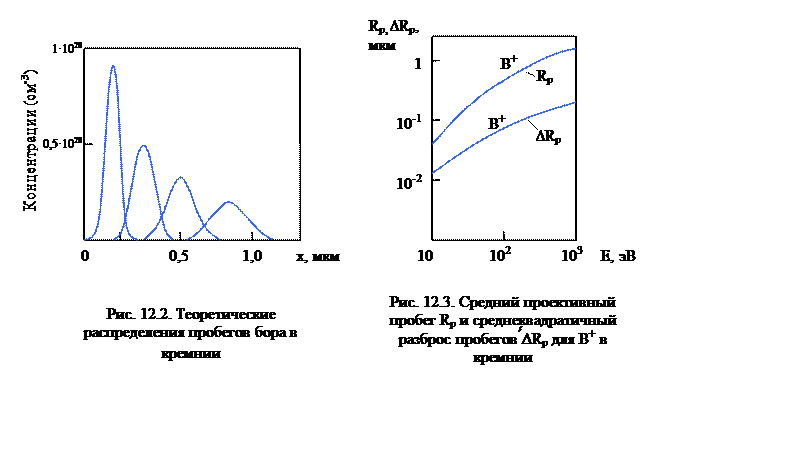
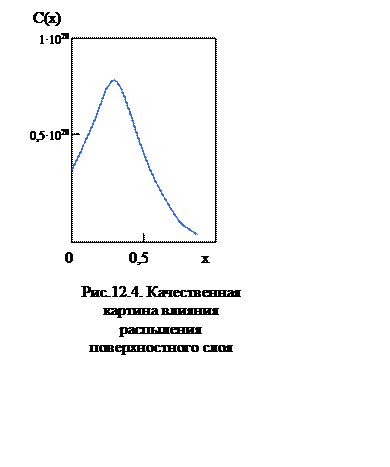
Функция распределения концентрации внедренных ионов по глубине образца, пропорциональная функции распределения пробегов отдельных ионов, в соответствии с экспериментальными данными (для невысоких доз облучения, когда можно пренебречь ионным распылением поверхностного слоя) и результатами численного моделирования процесса имплантации, может быть с хорошей точностью представлена гауссовским распределением

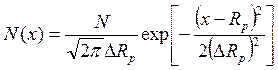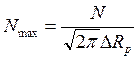,  ()                 (12.1)

Поскольку формула не учитывает обратного рассеяния ионов и распыления атомов матрицы, интеграл равен дозе облучения (флюенсу [1/см²] имплантированных атомов): .

12.3. Каналирование ионов.

Аморфное вещество                                             Монокристалл

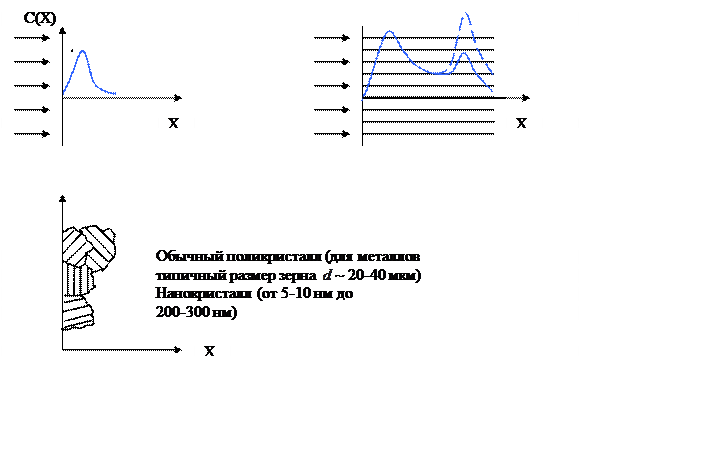
Рис.12.5. Иллюстрация к строению твердых тел.

Неожиданным результатом экспериментов, проводимых на поликристаллических мишенях, оказалось существование хвоста распределения внедрённых атомов до 5000Å (0,5 мкм). Этот эффект не наблюдается на аморфных материалах.

Компьютерное моделирование (выполненное в 60-е годы прошлого века) показало, что ~1 из 10⁴ траекторий особенно длинна, и вычислительная программа не всегда могла проследить до конца траекторию частицы. При внимательном изучении было установлено, что такие траектории расположены вдоль отдельных каналов между рядами наиболее плотноупакованных атомов. Эти каналы являются наиболее открытыми.

В ГЦК решетке Al, например, наиболее плотно упакованы ряды <110> (семейство направлений) и, следовательно, каналы между этими рядами (также в направлении <110>) наиболее открытые. Каналируемый (т.е. движущийся вдоль канала) атом передаёт свою энергию тысячам других атомов, не вызывая повреждений.

Прямые эксперименты были проведены Дэвисом на монокристаллах.

           

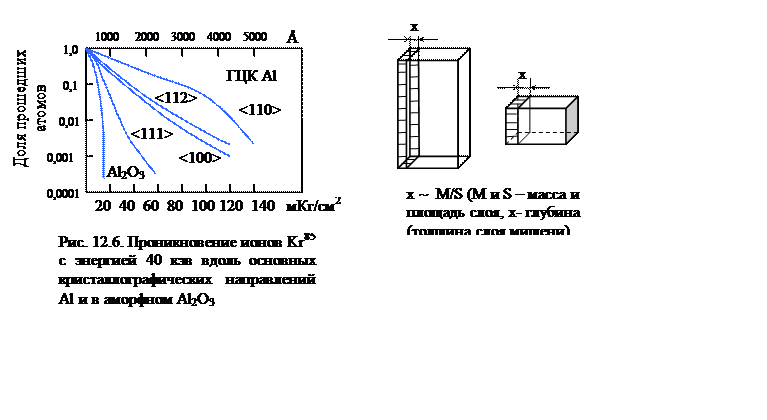
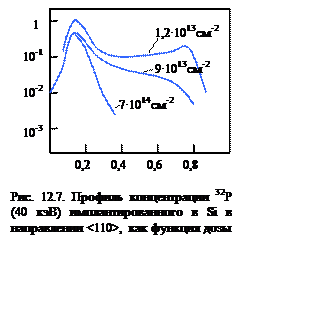
Каналирование естественно влияет на профиль концентрации ионов и на каскад атомных смещений, т.е. на профиль концентраций дефектов. Уменьшается число смещённых атомов на единицу пробега в начале пробега, а в конце пробега может возникать пик ионов и пик дефектов. Повреждения распределяются в большем объёме.

Вследствие каналирования появляется зависимость каскадной функции n(E₂)  от дозы, поскольку с увеличением дозы каналы “забиваются” примесями и каналирование ухудшается.

При каналировании в каскадах не происходит ядерных столкновений, потери обусловлены лишь возбуждением электронов и пробег пропорционален скорости ионов. Но использовать выражение  нельзя, т.к. оно для аморфной среды. Используют теорию Фирсова, а также Чешира и др.

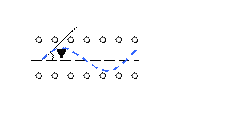
При каналировании частица движется между стенками канала из плотноупакованных атомов, отражаясь от них (чисто электростатический эффект).

Критический угол, под которым ион может войти в канал, не покидая его, оценил Линхард. Он ввёл скорости v_^ и v_║:

 

v║

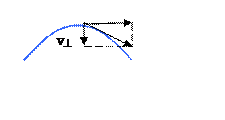
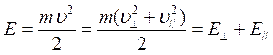                     (12.2)

Линхард считал, что величина E_^ должна быть меньше потенциала отталкивания от атомов цепочки V(r).

v

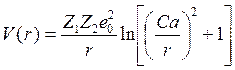,           (12.3)

Рис.12.7. Иллюстрация к эффекту каналирования где C ~ , а логарифмическое выражение это аппроксимация функции экранировки для потенциала типа потенциала Томаса-Ферми. Из E_^ = V(r) может быть рассчитано r_min

 

,                                                                                           (12.4)

                                                       ,                                             (12.5)

                                                               ,                                                   (12.6)

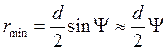                                                                                                         (12.7).

В результате подстановки (12.7) в (12.3) получаем уравнение, решение которого дает значение критического угла как функции энергии

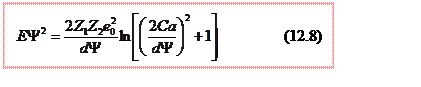
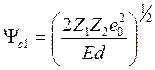
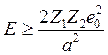),                            (12.8a)

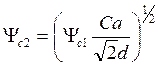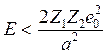().                          (12.8b)

Таблица 12.1

Критические углы каналирования бора в кремнии.

ион	Энергия кэВ	Критический угол, град.   *
		<100>	<110>	<111>
бор	10 100 300	4,76 2,67 2,03	6,97 3,47 2,98	5,30 2,98 2,26

*Максимальные возможные значения угла y допускающие каналирование (критические углы) для наиболее открытых каналов.