Методические указания для самостоятельной работы студентов по дисциплинам «Воздействие излучений на вещество» и «Электрофизические методы обработки материалов», страница 5

Для описания торможения ионов в веществе вводят понятия сечений   электронного и ядерного торможения S_е,_n

S_e,_n = -(1/N) (dE/dx)_e,_n ,                                                (1)

где dE/dx – потери энергии на единицу длины пробега иона (вследствие зависимости от энергии ионов эти потери изменяются по глубине мишени в ходе торможения), N – число атомов мишени в единице объема. Общий характер  зависимости электронного и ядерного торможения от энергии показан на рис. 1. Численные значения обозначенных на этом рисунке характерных энергий Е₁<E₂<E₃ для различных комбинаций ион-мишень содержатся в пределах: Е₁=1 – 10³ кэВ, Е₂=10–10⁴ кэВ, Е₃=10³–10⁶ кэВ. В области энергий Е<Е₃ торможение  ионов  описывается теорией Линдхарда-Шарфа-Шиотта (ЛШШ-теория), а при более высоких – теорией Бете-Блоха (H.Bethe, F.Bloch). При Е<E₂ преобладают ядерные потери, а при Е>E₂  – электронные.

В предположении о независимости процессов электронного и ядерного торможения ионов можно записать

– dE/dx = N [S_e(E)+S_n(E)].                                                (2)

Если зависимости S_e(E) и S_n(E) известны, то можно получить оценку средней общей длины пробега иона с начальной энергией Е  в аморфном теле

R = (1/N)  /(S_е(E)+S_n(E)) .                                            (3)

Теория ЛШШ дает для сечения электронного торможения соотношение S_e(E)=qE^1/2, где коэффициент q определяется значениями атомных масс и зарядов ядер бомбардирующих ионов и атомов мишени. Соотношение для S_n(E) является более сложным и задает зависимость c максимумом в точке Е₁ (рис.1).

Рис.1.  Сечения  электронного  S_e  и ядерного S_n  

торможения ионов как функция их энергии (схема)

Распределение пробегов. Профили концентрации внедренных ионов. Согласно теории ЛШШ пробеги ионов по глубине мишени описываются гауссовым распределением f(x)=exp[-(x-R_p)²/(2(ΔR_p)²)] и характеризуются средним проективным пробегом)\4 и стандартным отклонением ΔR_p, R_p (в дальнейшем для простоты - проективным характеризующим разброс значений пробегов (рис. 2, a). Вероятность того, что пробег иона находится в пределах от x до x+Δx (x – расстояние от поверхности мишени) равна произведению f(x)Δx. Значения R_p и ΔR_p согласно теории ЛШШ определяются энергией бомбардирующих ионов, а также соотношением порядковых номеров и атомных масс ионов и атомов мишени.

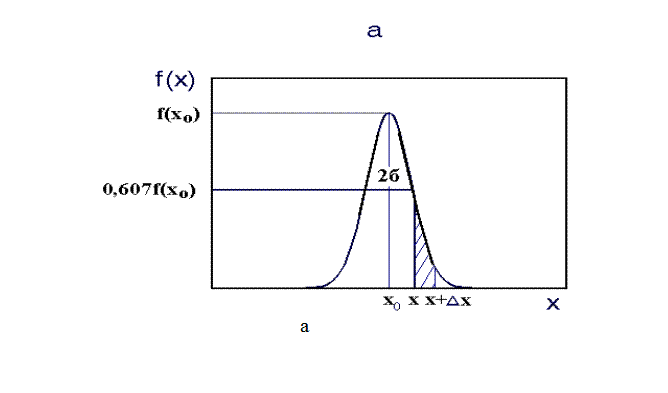
Pис.2.  Распределение пробегов ионов: а – функция  Гаусса  (гауссиан):  f(x)=1/(s) exp [- (x-x₀)² /2s²]; при  x₀=R_p  и s=DR_p   f(x) описывает предсказываемое теорией ЛШШ распределение имплантированных атомов по глубине мишени (заштрихованная площадь – вероятность того, что пробег иона заключен в интервале x+Dx; вся площадь под гауссовской кривой равняется единице); б – теоретические функции распределения пробегов (концентрационные профили) ионов B⁺ в Si.

Для того чтобы от распределения пробегов перейти к распределению концентрации внедренной примеси с(x) по глубине мишени достаточно f(x) умножить на значение флюенса с(x) = F f(x), см^-3. Кривые с(x) называются профилями концентрации внедренной примеси или концентрационными профилями. На рис. 2,b распределение пробегов представлено как раз в виде профилей концентрации примесей.

Для кристаллических мишеней может наблюдаться заметное отклонение экспериментально наблюдаемых профилей распределения ионов по глубине от расчетных, вследствие рассматриваемых ниже эффектов ионного каналирования, распыления поверхностного слоя падающими ионами и радиационно-усиленной диффузии.

Образование радиационных дефектов. Процесс упругого соударения ионов с ядрами (атомами) мишени сопровождается, в зависимости от энергии и массы имплантированных ионов, а также массы атомов мишени, выбиванием большего или меньшего числа атомов из их устойчивых положений в твердом теле. В периодических кристаллах такими устойчивыми положениями являются положения атомов в узлах кристаллической решетки. Выбитые со своих мест атомы при наличии у них достаточной энергии могут, в свою очередь, смещать другие атомы, т.е. вызывать каскад атомных смещений. Это приводит к накоплению вблизи траекторий ионов вакансий и междоузельных атомов (пар Френкеля) и сложных дефектов решетки – кластеров.