Расчет и конструирование пустотной панели перекрытия

Расчет и конструирование пустотной панели перекрытия.

Исходные данные

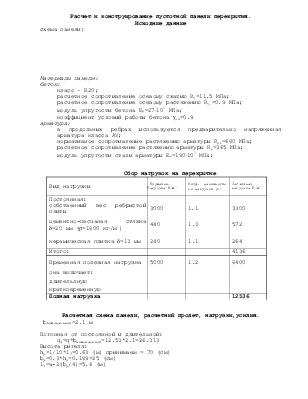
схема панели:

Материалы панели:

бетон:

класс – В20;

расчетное сопротивление осевому сжатию R_b=11.5 МПа;

расчетное сопротивление осевому растяжению R_bt=0.9 МПа;

модуль упругости бетона E_b=27×10³ МПа;

коэффициент условий работы бетона g_b2=0.9

арматура:

в продольных ребрах используется предварительно напряженная арматура класса АV;

нормативное сопротивление растяжению арматуры R_sn=680 МПа;

расчетное сопротивление растяжению арматуры R_s=365 МПа;

модуль упругости стали арматуры E_s=190×10³ МПа;

Сбор нагрузок на перекрытие

Вид нагрузки	Норматив. Нагрузка Н/м2	Коэф. надежности по нагрузке gb2	Расчетная нагрузка Н/м2
Постоянная:
собственный вес ребристой плиты	3000	1.1	3300
цементно-песчаная стяжка d=20 мм (r=1800 кг/м3)	440	1.3	572
керамическая плитка d=13 мм	240	1.1	264
Итого:			4136
Временная полезная нагрузка	5000	1.2	8400
она включает:
длительлную
кратковременную
Полная нагрузка			12536

Расчетная схема панели, расчетный пролет, нагрузки,усилия.

b_{номинальное}=2.1 м

Погонная от постоянной и длительной:

q_l=q*b_{номинальное}=12.53*2.1=26.313

Высота ригеля:

h_р=1/10*l_Р=0.63 (м) принимаем = 70 (см)

b_р=0.3*h_р=0.189=25 (см)

l₀=a-2(b_р/4)=5.6 (м)

Усилия от расчетной нагрузки:

M=q₁^p×L₀²/8=26.313×5.6²/8=97.99 кН×м

Q=q₁^p×L₀/2=26.313×5.6/2=69.99 кН

Размеры сечения плиты

b=b_н-5см=2.1-0.5=205 (см)

Высота плиты:

h=22 (cм)

Количество пустот:

n=11

Количество рёбер:

n_рёб=12

сумма b_рёб=b-n*15.9=205-11*15.9=30.1 см –расчетная ширина сечения;

b_рёб=сумма b_рёб/n_рёб=30.1/12=2.5 (см) Þ принимаем = 2.4 (см)

b_кр.рёб=(30.1-2.4)/2=3.05

h₀=h-a=22-3=19 см – рабочая высота сечения;

h_f’=3 см – толщина верхней сжатой полки таврового сечения;

Условия работы всей ширины полки:

1)  

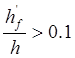
3.1/22=0.14 >0.1-условие выполнено

2)  

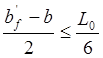
(202-30.)/2=85.95 <0.93 (см)

Оба условия выполнены в расчет принимаем всю ширину полки b_f’=b_k=202 см

Расчет прочности нормального сечения

Определяем расчетный случай:

если M<M_f значит первый расчетный случай

M_f=g_b2×R_b×b_f¹×h_f¹×(h₀-h_f¹×a)=0.9×11.5×202×3.1×(19-3.1/2)=113.096(Н×см)

98<113.096 – имеем первый расчетный случай - нейтральная ось лежит в области сжатой полки.

Панель предварительно напряженная с одиночным армированием .Далее подбираем диаметр и количество стержней рабочей продольной арматуры.

a_m=M/(g_b2×R_b×b_f’×h₀²)=97.99/(11.5×0.9×202×19²)=0.13

зная a_m по таблице подбираем x=0.14,z=0.93

Определяем x_R:

x_R=W/(1+ s_SR/500(1-W/1.1))=0.758/(1+511/500(1-0.758/1.1)=0.59

W=0.85-0.008R_b=0.85-0.008*11.5=0.758

s_SP=0.75*590=443 (Мпа)

P=30+360/l=30+360/6=90 (Мпа)

s_SP+P=443+90=533< R_sn=590 (Мпа)-условие выполняется

s_SR= R_s+400-s_SP*g_SP=510+400-443*0.9=511 (МПа)

Определяем коэффициент g_S6 учитывающий особенности работы высокопрочной арматуры :

g_S6=h-(h-1)(2x/x_R-1)=1.2-(1.2-1)(2×0.14/0.59-1)=1.3

здесь h=1.2 для арматуры класса А3

g_S6 не может быть больше 1.2 принимаем g_S6=1.2

Находим требуемую площадь сечения растянутой арматуры :

A_S=M/(g_S6×R_S×z×h₀)=98/(1.2×510×0.93×19)=9.06 см²

По таблице подбираем ближайшую площадь A_S=9.23 см² которую составляют 6 стержней диаметра 14 мм.

Расчет продольных ребер на прочность наклонных сечений.

Усилие обжатия:

N=A×s_sp здесь:

A_S=9.23 см²

                              s_sp=0.8×R_sn=0.75×590=443 МПа

N=9.23×10²(443)=408.889 кН

Определяем коэф. учитывающий усилие обжатия:

f_n=0.1×N/(R_bt×b×h₀)  <0.5

f_n=0.1×408889/(0.9×30.1×19×100)=0.8 >0.5Þ принимаем =0.5

k=1+f_n+f_f=1+0.04+0.8=1.84>1.5

f_f=0/75(b_f¹-b)h_f¹/(bh₀)=(0.75(3.1*3)*3.1)/30.1*19=0.04<0.5

b_f¹<b+3h_f¹=30.1+3*3.1=39.4 (см)

Q_{b min}=f_b3kR_btbh₀=0.6*1.5*0.9*30.1*19=46.3<70 кН

Принимаем S=10см

q_sw=R_swf_swn/S=175*1.539*100/10=2058Н/см

q_sw ³Q_{b min}/2h₀=46.3*1000/(2*19)=1218 н/см

M_b= f_b2kR_btbh₀=2*1.5*0.9*30.1*19²*100=29.3*10⁵ (Н/см)

q₁<0.56q_sw=263.13<1152

c=ÖM_b/q₁=105.5

с<(f_b2/f_b3)h₀=2/0.6*19=63.3>105.5 Þпринимаем с=63.3 см

Q_b=M_b/C=29.3/63.3=46.5*10³(Н)

Длина проекции расчетного наклонного сечения:

38см <2ho=2·19=38 см, принимают сo=38 см.

При этом Qsw=qsw·co=2058·38=78,2·10³ Н

Условие:

Q=Q_MAX-q₁×C=70×10³-26.3×63.3=68.3 кН

Условие прочности:

Qb+Qsw=46.3·10³+78.2·10³=124.5·10³ Н>Q=68.3·10³ Н-обеспечивается.

Прочность проверяют по сжатой наклонной полосе.

μsw=Asw/bs=6*0.196/30.1·10=0,003;     α=Es/Eb=190000/27000=7;

φw1=1+5αμsw=1+5·7·0,0039=1,14                                                             β=0,01- тяжелый бетон  ;   φb1=1-βRb=1-0,01·11,5   =0,885             

Условие прочности:                          

0,3φb1φw1Rbbho=0,3·1.14·11,5(100)·19·30.1·0.885=199·10³Н>Qmax=70·10³Н-обеспечивается.

f_b4×(1+f_n)×R_bt×b×h₀²/C=1.5×(1+0.5)×0.9×0.9×100×30.1×19²/47.5=41.7 кН

41.7 < 66 – не удовлетворяется, Þ поперечная арматура требуется по расчёту.

На приопорных участках длиной (L/4) арматура устанавливается конструктивно- четыре диаметра по 4 мм марки Вр-I с шагом S=10 см,в середине пролета арматура не ставится.

Расчет ригеля.

Расчетная схема, расчетный пролет,нагрузки,усилия.

Исходные данные:

Ригель работает как однопролетная шарнирно опертая балка.

бетон:

класс – В20;

расчетное сопротивление осевому сжатию R_b=11.5 МПа;

расчетное сопротивление осевому растяжению R_bt=0.9МПа;

модуль упругости бетона E_b=27×10³ МПа;

коэффициент условий работы бетона g_b2=0.9;

арматура:

класс АIII;

расчетное сопротивление растяжению арматуры R_s=365 МПа;

расчетное сопротивление растяжению поперечной арматуры R_sw=290 МПа;

расчетный пролет:

L₀=L-2×(h_k/2+a+L₁/2)=6300 -2×(300/2+50+75)=5750 мм

Нагрузка на ригель от панелей считается равномерной.

Расчетная нагрузка на метр длины ригеля:

q=(g+V)×a×g_n+g_риг

g_риг=b×h×g_f×g_б=25×0.189×0.63×1.1=3.27кН/м

q=12.53×5.7=71.421кН/м здесь:    g_f=1.1 – коэф. надежности по материалу

g_n=0.95 – коэф. надежности по назначению здания

Определяем максимальные усилия в ригеле:

М_max=q×L₀²/8=74.691×5.75 ²/8=293 кН/м

Q_max=q×L₀/2=74.691×5.75/2=204 кН

Расчет прочности нормальных сечений.

Т.к. профиль ригеля – тавр с полкой в растянутой зоне за расчетное принимаем прямоугольное сечение.

Z_b=h₀-0.5×x

h₀=h-a_з=70-6=64 см

a_m=M/(g_b2×R_b×b×h₀²)=293000/(0.9×11.5×25×64²)=0.275

по таблице подбираем :

a_m=0.262  x=0.33    z=0.835

Площадь сечения арматуры :

A^тр_S=M/(R_S×h₀×z)=293000/(355×64×0.835)=15.4 см²

По таблице подбираем – 4Æ22 с площадью 15.2 см²

Расчет прочности наклонных сечений.

Диаметр поперечных стержней устанавливаем по условию сварки с продольной арматурой диаметра 28мм и по таблице принимаем 8 мм.Площадь А_sw=0.196 см² ,класс АIII ,R_sw=285МПа.

g_b2=0.9 – коэф. условий работы , с его учетом R_SW=0.9×285=255 МПа.

Количество каркасов – 2 площадь A_s=1 см²

Шаг поперечных стержней по конструктивным условиям:

S=h/3=70/3=20 см – принимаем на приопорных участках длиной L/4

S=3/4×h=50 см – шаг стержней в средней части ригеля

Погонное усилие в поперечных стержнях:

q_sw= R_sw× А_sw/S=255×0.196×2(100)/20=499.8 Н/см

Q_b,min=f_b3×R_bt×b×h₀=0.6×1×0.9×25×64=86.4 кН

Условия:

1)   q_sw> Q_b,min/(2×h₀)

499.8 < 675 – условие не выполнилось,принимаем q_sw=675 н/см

2)  S_max>25 см

S_max=f_b4×R_bt×b×h₀²/Q=

=1.5×0.9×25×64²×(100)/204000=68 см

68>25 – условие выполнено

3)  q₁<0.56×q_sw=675×0.56=378 кН/м

263.13<378 – условие выполнено

Вычисляем поперечную силу Q_b , воспринимаемую бетоном сжатой зоны над наклонным сечением:

Q_b=М_b/С

M_b=f_b2×R_bt×b×h₀²=2×1×0.9×25×64²×(100)=184×10⁵ Н×см

С=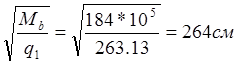 >213.3 cм, принимаем с=213.3

Q_b=184×10⁵/213.3=86700 Н

Q_b=86700 Н > Q_b,min=86400 Н – условие выполнено.

Определяем длину проекции наклонного сечения:

С₀=165 см

Ограничения:

1)  С₀<С=213.3 – выполнено

2)  С₀<2×h₀=128 – не выполнено

3)  С₀>h₀=64 – выполнено принимаем С₀=128.

Поперечная сила в верху наклонного сечения:

Q=Q_max-q₁×C=204-263.13×213.3=148 кН

Находим поперечную силу воспринимаемую хомутами в наклонном сечении:

Q_sw=q_sw×C₀=128×675=86 кН

Проверяем условие прочности:

Q < Q_b+Q_sw

148 < 86.7+86=172.7 – условие выполнено

Проверка прочности по сжатой полосе между наклонными трещинами:

m_w=A_sw/(b×S)=0.00078

a=E_s/E_b=200000/27000=7

f_w1=1+5×a×m_w=1.03

f_b1=1-0.01×R_b=1-0.01×11.5=0.885

Условие прочности:

Q_max<0.3×f_w1×f_b1×R_b×b×h₀=0.3×1.03×0.885×11.5×25×64

204<503 – условие прочности выполнено.

Расчет и конструирование колонны среднего ряда первого этажа.

Материалы колонны:

бетон:

класс – В20;

расчетное сопротивление осевому сжатию R_b=11.5 МПа;

расчетное сопротивление осевому растяжению R_bt=0.9 МПа;

модуль упругости бетона E_b=24×10³ МПа;

арматура:

класса АIII

расчетное сопротивление растяжению арматуры R_s=365 МПа;

модуль упругости стали арматуры E_s=200×10³ МПа;

Сбор нагрузок на колонну, определение расчетного усилия.

Грузовая площадь приходящаяся на одну колонну :

А_груз=L_ригеля×а=6.3×5.7×5.48=197 кН

Вес ригеля:

q_риг=3.27×6.3=20600 Н

2Q₁=197+20.6=217.6 кН

G₁=0.3*0.3*3.9*25*1.1=9.6525 кН

G₂=0.3*0.3*3.35*25*1.1=8.29 кН

N=2×204×5+217.6+9.65×5+8.29=2314.14 кН

Расчет продольной арматуры.

Принимаем симметричное армирование: А_s=A_s'

сечение колонны: h×b=30×30=900 см²

защитный слой - а_з=4 см рабочая высота сечения: h₀=h-a_з=30-4=26 см расчетная длинна колонны: L₀=0.7×h_эт=0.7×2.78=1.946 м

Находим случайный эксцентриситет силы:

Из следующих трех значений выбираем максимальное :

1 е_а=h/30=30/30=1 см

2 е_а=L₀/600=194.6/600=0.32 см

3 е_а=1см

Принимаем е_а= 1см

Эксцентриситет силы е_о=N_дл/N=1 см

Определяем величину критической продольной силы:

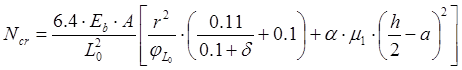
d=e₀/h=1/30=0.03

d_min=0.5 - 0.01×L₀/h - 0.01×R_b =

=0.5 - 0.01×(194.6/30) - 0.01×14.5=0.3

d<d_min (0.03<0.3) –принимаем d=0.3

a=E_s/E_b=200×10³/27×10³=7 – отношение модулей упругости

m₁=2×A_s/A=0.02– коэф. армирования зададим предварительно.

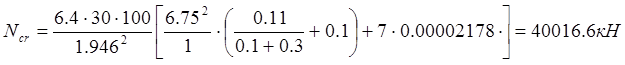
Находим коэф. h=1/(1-N/N_cr)=1/(1-2317.45/40016.6)=1.06

Опредляем е=е_о×h+h/2-a_з=1×1.06+30/2-4=16 см

Граничная относительная высота сжатой зоны:

x_R=w/(1+s_SR/s_S×(1-w/1.1)) здесь:

w=0.85-0.008×R_b=0.85-0.008×0.9×14.5=0.734–характерезует деформационные свойства тяжелого бетона сжатой зоны.

x_R=0.734/(1+365/500×(1-0.734/1.1))=0.59

Находим a_n=N/(R_b×b×h₀)=2314.14/(14.5×30×26)=2.046> x_R=0.59

x=(a_n×(1-x_R)+2×a_s×x_R) / (1-x_R+2×a_s)

a_s=a_n×(e/h₀-1+a_n/2) / (1-d')=

=2.46×(16/26-1+2.046/2)/(1-0.154)=1.54>0.59 – принимаем А_s=A_s' конструктивно по минимальному проценту армирования.

Принимаем 2Æ36 AIII c A_s=20.36 см²

Проектирование консоли колонны.

Размеры опорной консоли:

с=5 см – зазор между торцом ригеля и гранью колонны.

Наименьший вылет консоли с учетом зазора принимаем L₁=250 мм;

L_оп=200 мм – площадка опирания;

высота консоли h=500 мм;

Находим опорное давление ригеля Q=q_риг×L₀/2 где

L₀=L-2×D=7-2×0.3=6.4 – расчетный пролет ригеля

Q=52.82×6.4/2=162.63 кН

Выполняем проверку прочности консоли на смятие:

Q < R_b,см×L_оп×b_риг×0.75 здесь:

b_риг=30 см – ширина ригеля; коэф. 0.75 учитывает неравномерность смятия

R_b,см=a×f_b× R_b=1×1×11.5 МПа(a=1 – коэф. учитывающий класс бетона , f_b=1 – коэф. учитывающий распределение нагрузки)

162.7<11.5×(100)×200×300×0.75=622.5 кН – условие выполнено расчетная длина площадки смятия удовлетворяет условию , прочность на смятие обеспечена.

Выполняем проверку консоли на прочность от главных сжимающих напряжений (т.е. по наклонной сжатой полосе между силой и опорой) по условию:

Q<0.8×f_w2×R_b×b_к×L_оп×sinQ, где f_w2=1+5×a×m_w1- коэф. учитывающий влияние хомутов, расположенных на высоте колонны.

a=E_s/E_b=200×10³/24×10³=8.3

m_w1=A_sw/(b_к×S_w)=0.566/(30×10)=0.00189

A_sw-площадь сечения хомутов в одной плоскости,т.е. для 2-х стержней d=6 мм AI в горизонтаьной плоскости A_sw=2×0.283=0.566 см²

b_к=30 см – ширина коноли, равная ширине ригеля

S_w-шаг хомутов принимаем минимальный из следующих условий:

S_w<150мм

S_w<h_k/4=500/4=125

принимаем S_w=100 мм

f_w2=1+5×8.3×0.00189=1.078

sinQ=L₁/K=L₁/= 250/

Проверяем условие:

162.63<0.8×1.078×11.5×0.9×30×20×0.447×(100)=255.5кН–прочность обеспечена

Это условие ограничивается:

0.6×R_bt×b×h₀<255.5<3.5×R_bt×b×h₀ здесь h₀=50-3=47 см

68.5кН<255.5<399.7- условие ограничения выполняется

Найдем изгибающий момент консоли у грани колонны по формуле:

M=Q×a=162.63×15=2439 кН×см здесь а=L₁-L_оп/2=250-200/2=150см – расстояние от грани колонны до точки приложения силы Q

Вычислим площадь сечения продольной арматуры:

A_s=1.25×M/(R_s×x×h₀) где x=0.9

A_s=1.25×2439/(365×0.9×47×(0.1))=1.97см²

Принимаем 2Æ12 AIII , A_s=2.26 см²

 

Расчет стыка колонн.

Стык двух колонн выполняется на расстоянии 500-900 мм от пола этажа. Арматура в стыке сваривается ванной сваркой. Из условия сварки диаметр свариваемой арматуры > 20 мм. После сварки стык замоноличивают бетоном под давлением . Класс бетона тот же что и в колонне . Расчет выполняется в стадиях монтажа и эксплуатации.

1 стадия эксплуатации

а) расчет без учета косвенного армирования производится по условию:

N_стык<N_сеч=N^к_b+N_b^замон +N_s

Определяем:

N_сеч= R^к_b×A^к_b×0.9+0.8×R^з_b×A^з_b+R_sc×A_s

N_сеч=0.9×11.5×(100)×(30×30-9×9×4)+0.8×11.5×100×(9×9×4)+ 2×6.28×365×100=1.055×10⁶ Н=1055 кН

941<1055 – условие выполнено, значит арматуру сеток С-1 принимаем конструктивно d=10мм, AIII, R_s=365МПа

2 стадия монтажа

Прочность проверяется без учета бетона замоноличивания, но с учетом работы центрирующего выступа с косвенным армированием в виде поперечных сеток, и арматурных выпусков , соединенных ванной сваркой.

Расчет производится из условия:

N_стык<N_{ядра сеч}+N_s

N_{ядра сеч}=0.9×R_b,red×A_lf  здесь: R_b,red = R_b×f_b+ f×m_s×R_s

m_s- коэф объемного армирования.

m_s=V_s/V_b=(h₁×L₁×A_s+ h₂×L₂×A_s)/A_lf×S

m_s=(6×27×0.785+8×9×0.785)/405×6=0,0756

Находим коэф. эффективности объемного армирования:

f=1/(0.23+y) здесь

y=m_s×R_s/(R_b+10)

y=0.0756×365/(11.5+10)=1.283

f=1/(0.23+1.283)=0.66

R_b,red = 11.5+0.66×0.0756×365=29.712

N_{ядра сеч}+N_s=0.9×29.712×(0.1)×405+365×(0.1)×2×6.28=1541кН

941<1541- условие выполняется.Прочность обеспечена.

Еще одно условие прочности

N_монт<0.75×N_смятия+N_s×f₁×0.5   здесь

N_монт- расчетное усилие в период возведения первого перекрытия