Регрессионный анализ в системе Statistica

Практика 12 (часть II).

Регрессионный анализ в системе Statistica.

В первой части мы отметили, что для проведения регрессионного анализа в системе Statistica пользователю предлагается два модуля – Множественная регрессия (Multiple Regression) и Нелинейное оценивание (Nonlinear Estimation).

Модуль Множественная регрессия был разобран в предыдущей части.

Работу модуля Нелинейное оценивание (Nonlinear Estimation) рассмотрим на следующем примере.

Пример 2. По следующим данным найдите наилучшие оценки параметров в уравнении:

.

Определить 95%-е доверительные интервалы для параметров.

Данные:

y	-4,8	-3,0	-4,2	20,0	53,4	51,6
x	95,9	48,2	19,5	5,4	1,4	0,4

Шаг 1. Введем данные в файл и присвоим им соответствующие имена Y и X.

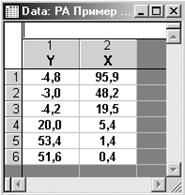
Шаг 2. Визуализируем данные: Graths / 2D Graphs / Scatterplots.

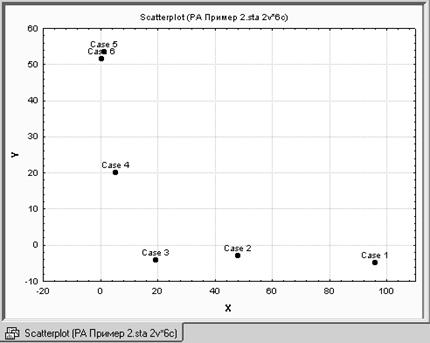
Шаг 3. Запустим модуль Нелинейное оценивание (Nonlinear Estimation).

определяемая пользователем регрессия:

методом наименьших квадратов (по умолчанию)

с выбором функции потерь

Выбираем закладку User-specified regression, custom loss function.

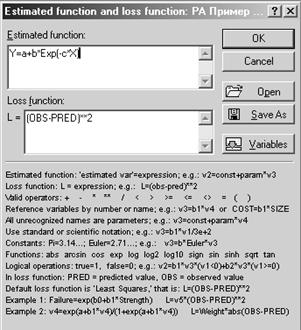Шаг 4. В окне Оцениваемая функция вводим нашу исходную функцию. Функция потерь (Loss functoin) по умолчанию определена как сумма квадратов разностей наблюдаемых и предсказанных значений [(OBS-PRED)**2], следовательно, оценки параметров вычисляются методом наименьших квадратов. Понятно, что функцию потерь можно задать любой произвольной формы.

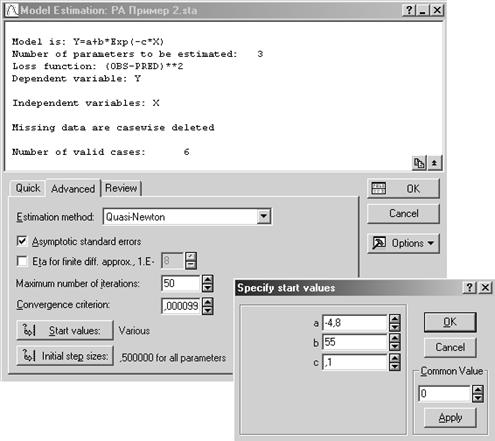Шаг 5. В открывшейся панели Model Estimation (метод оценивания) выбирается вычислительный метод, например, Quasi-Newton, можно задать начальные значения параметров (Start values), число итераций (Maximum number of iterations), шаг изменения параметров (Initial step sizes). Чтобы получить среднеквадратические оценки параметров нужно включить опцию Asymptotic Standard errors.

Шаг 6. После ввода всех необходимых значений, получаем следующие результаты.

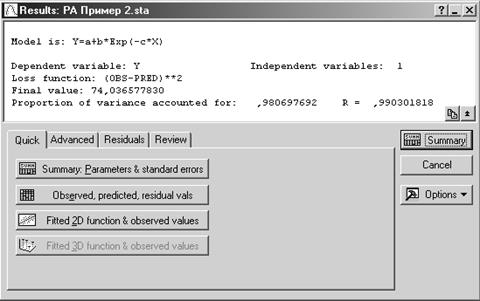
Окончательное значение

функции потерь: 74,04

коэффициент детерминации: 0,98

Шаг 7. Нажав кнопку Fitted 2D function… на панели результатов, получим график функции и исходных данных:

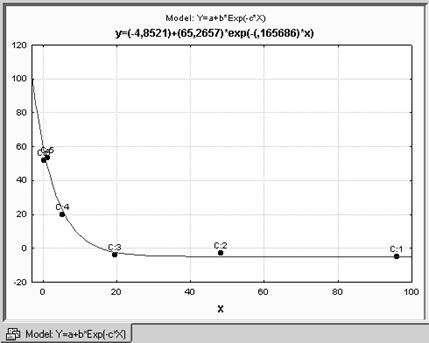
Шаг 8. Оценки параметров, их среднеквадратические значения, t-статистики и соответствующие уровни значимости выводятся при нажатии кнопки Parameters & Standard errors.

График функции и значение коэффициента детерминации говорят о том, что модель адекватна результатам наблюдений.

Задания для самостоятельной работы.

Задача №8. Найдите значения параметров a и b функции Кобба-Дугласа:

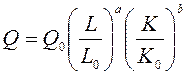, где Q – объем производства; L – трудовые ресурсы; K – капитал; а Q₀, L₀, K₀ – фиксированные значения этих переменных: Q₀ = 51, L₀ = 19, K₀ = 16.

Значения Q при определенных трудовых ресурсах L и стоимости капитала K заданы в таблице:

K L	6	11	16	21	26
9	6	12	19	27	36
14	11	12	35	50	66
19	17	32	51	72	96
24	22	42	67	95	126
29	27	52	83	118	156

Задача №9. Прибыль P, получаемая фирмой, определяется формулой Р=kx-c, где х – объем производства (т), k – цена одной тонны продукции (руб./т), с – издержки производства (руб.).

Предположим, что k = 40 руб./т, а переменные х и с имеют следующие значения:

х	0	1	2	3	4	5	6	7	8	9	10	11
с	50	100	128	148	162	180	200	222	260	305	360	425

Найдите оценки параметров модели P(x):

P(x) = β₀ + β₁x + β₂x² + β₃x³.

Сравнить полученные данные с результатами задачи №5 (Практика 12 (часть I)).

Задача №10. Приведенные ниже данные представляют значения трех зависимых переменных y₁, y₂, y₃ и независимой переменной x. Найдите оценки параметров a и b для следующих моделей:

, i = 1, 2, 3.

Проверьте, хорошо ли подходит к этим данным полиномиальная модель?

x	y1	y2	y3
1,0	9,0	4,4	6,7
2,0	9,0	8,1	12,5
3,0	16,0	9,4	14,3
4,0	20,0	10,2	15,8
5,0	21,0	12,3	17,1
6,0	22,0	11,5	18,0
7,0	23,0	13,2	20,0
8,0	30,0	15,2	36,3
9,0	41,0	18,5	45,1
10,0	50,0	31,0	60,0

Задача №11. Найдите оценки параметров a, b, c для модели:

по следующим данным: