

Практика 06 (часть II).
Однофакторный дисперсионный анализ. Группировка данных по классифицирующему признаку.
6.2. Однофакторный дисперсионный анализ.
Основные понятия.
Пусть результаты наблюдений составляют n независимых выборок (групп), полученных из n нормально распределенных генеральных совокупностей, которые имеют различные средние и равные дисперсии. Проверяется гипотеза о равенстве средних.
На практике такая задача возникает при исследовании влияния, которое оказывает изменение некоторого фактора на измеряемую величину. Например, если измерения проводятся на n различных приборах, то можно исследовать влияние фактора «прибор» на результаты измерения.
Пример 2. Удобрения для комнатных растений фасуются в пакеты весом по 0,5 кг. Из партии пакетов, расфасованных в течение суток, случайным образом отобрали 30 пакетов. Они распределены по трем различным условиям хранения. После хранения в течение одной недели определялось содержание влаги в продукте, хранящемся в каждом пакете.
Данные содержания влаги приводятся ниже.
|
условия хранения |
содержание влаги, % |
|
1 |
10,1; 7,3; 5,6; 6,2; 8,4; 8,1; 8,0; 7,6; 5,3; 7,2 |
|
2 |
11,7; 12,2; 11,8; 7,8; 8,9; 9,9; 12,4; 11,0; 10,3; 13,8; 10,5; 9,8; 9,1 |
|
3 |
10,2; 12,0; 8,8; 8,7; 10,5; 11,0; 9,1 |
На уровне значимости α = 0,05 проверить гипотезу о том, что условия хранения продукта не оказывают влияния на содержание влаги.
Предполагается, что выборки получены из независимых нормально распределенных совокупностей с одной и той же дисперсией.
Шаг 1. Создайте файл с исходными данными и запустите Группировка и однофакторный дисперсионный анализ (Breakdown & one-way ANOVA).
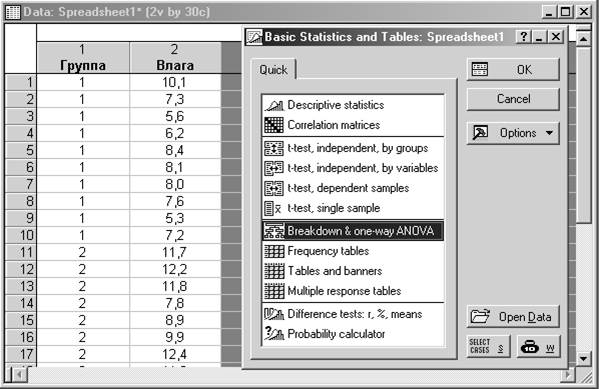
Шаг 2. Укажите как группирующую переменную столбец Группа, а как зависимую переменную – Влага.
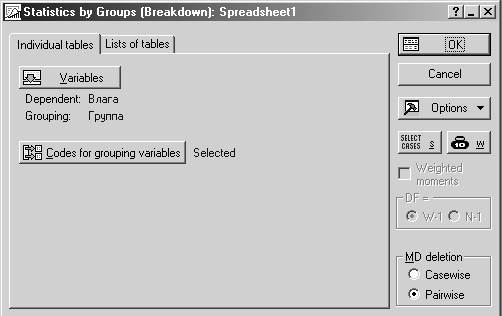
Шаг 3. В окне результатов в закладке ANOVA & tests необходимо нажать кнопку Analysis of Variance (дисперсионный анализ). Не забудьте задать необходимый уровень значимости.
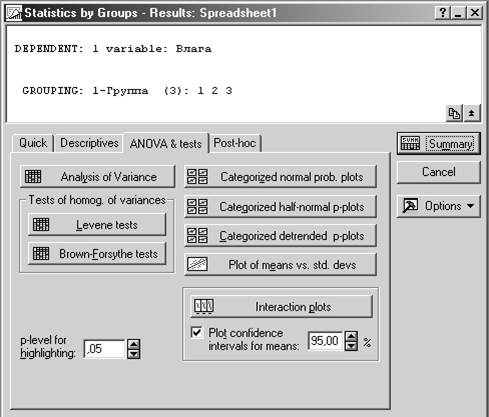
Критерии однородности дисперсий:
критерий Левена
критерий Брауна-Форсайта
Шаг 4. В таблице дисперсионного анализа приводятся:
SS Effect – сумма квадратов отклонений выборочных средних групп от общего среднего (Q1);
df Effect – число степеней свободы для Q1;
МS Effect – среднее значение суммы квадратов (отношение Q1 к числу степеней свободы для Q1);
SS Error – сумма квадратов отклонений результатов наблюдений от выборочных средних групп (Q2);
df Error – число степеней свободы для Q2;
MS Error – среднее значение суммы квадратов (отношение Q2 к числу степеней свободы для Q2):
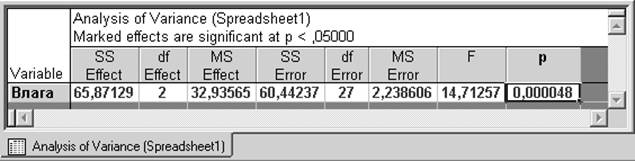
Далее приводятся:
F – выборочное значение F-статистики;
p – вычисленный уровень значимости.
Так как вычисленный уровень значимости р = 0,000048 меньше заданного уровня значимости α = 0,05, то гипотеза о равенстве средних отклоняется. Таким образом, условия хранения продукта значимо влияют на содержание влаги в продукте (все значения выделены красным цветом).
Шаг 5. Напомню, что при применении дисперсионного анализа предполагается, что исходные данные – независимые выборки наблюдений, полученные из нормально распределенных генеральных совокупностей, имеющих одну и ту же дисперсию. При выполнении анализа выполнение этих предположений можно проверить.
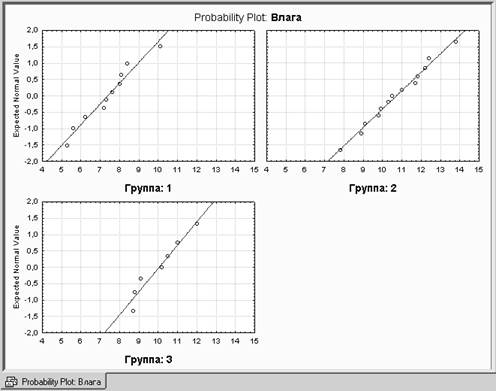 Один из способов проверки
нормальности состоит в том, что строится специальный график (кнопка Categorized normal prob. plots – категоризованные нормальные вероятностные графики)-
точки, соответствующие нормально распределенным данным, укладываются на прямые.
Один из способов проверки
нормальности состоит в том, что строится специальный график (кнопка Categorized normal prob. plots – категоризованные нормальные вероятностные графики)-
точки, соответствующие нормально распределенным данным, укладываются на прямые.
Как показывают графики, исходные данные достаточно плотно группируются относительно прямых.
Для проверки выполнения предположения о равенстве дисперсий по группам используются так называемые критерии однородности дисперсий (Test of Homog. of Variances).
В пакете для этих целей можно использовать критерий Левена (Levene tests), либо критерий Брауна-Форсайта (Brown-Forsythe tests).
Чтобы выполнить эти процедуры нужно нажать соответствующие кнопки в окне результатов дисперсионного анализа. Для исходных данных примера гипотеза о равенстве дисперсий по группам принимается по этим двум критериям на уровнях значимости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.