Непараметрическая статистика. Таблицы частот (сопряженности) 2×2. Наблюдаемые частоты в сравнении с ожидаемыми. Корреляции

Практика 08 (часть I).

Непараметрическая статистика.

Одним из факторов, ограничивающих применения критериев, основанных на предположении нормальности, является объем выборки. До тех пор пока выборка достаточно большая (например, 100 или более наблюдений), можно считать, что выборочное распределение нормально, даже если вы не уверены, что распределение переменной является нормальным. Тем не менее, если выборка мала, эти критерии следует использовать только при наличии уверенности, что переменная действительно имеет нормальное распределение. Однако нет способа проверить это предположение на малой выборке.

Использование критериев, основанных на предположении нормальности, кроме того, ограничено шкалой измерений. Такие статистические методы, как t-критерий, регрессия и т.д., предполагают, что исходные данные непрерывны. Однако имеются ситуации, когда данные, скорее, просто ранжированы (измерены в порядковой шкале), чем измерены точно.

Типичный пример дают рейтинги сайтов в Интернете. Представьте, вы имеете 5 сайтов: A,B,C,D,E, которые располагаются на 5 первых местах. Пусть в текущем месяце мы имели следующую расстановку: A,B,C,D,E, а в предыдущем месяце: D,E,A,B,C. Спрашивается, произошли существенные изменения в рейтингах сайтов или нет? В данной ситуации, очевидно, мы не можем использовать t-критерий, чтобы сравнить эти группы данных, и переходим в область специфических вероятностных вычислений. Мы рассуждаем примерно следующим образом: насколько велика вероятность того, что отличие в двух расстановках сайтов вызвано чисто случайными причинами или это отличие слишком велико и не может быть объяснено за счет чистой случайности. В этих рассуждениях мы используем лишь ранги или перестановки сайтов и никак не используем конкретный вид распределения числа посетителей на них.

Для анализа малых выборок и для данных, измеренных в бедных шкалах, применяют непараметрические методы.

Стартовая панель модуля имеет вид (Statistics/Nonparametrics):

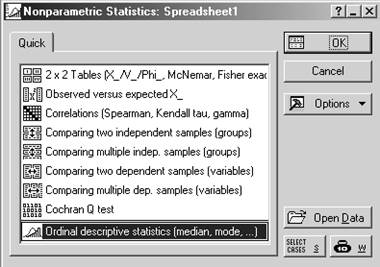
Таблицы 2×2: хи/V/фи, Макнемара, точный Фишера

Наблюдаемые частоты в сравнении с ожидаемыми

Корреляции (Спирмена, тау Кендала, гамма)

Сравнение двух независимых выборок (группы)

Сравнение нескольких независимых выборок

Сравнение двух зависимых выборок (переменные)

Сравнение нескольких зависимых выборок

Q критерий Кохрена

Обычные описательные статистики

Перед тем, как приступать к описанию и разбору непараметрических процедур на примерах, необходимо провести краткий обзор непараметрических процедур.

8.1. Таблицы частот (сопряженности) 2×2: статистики хи/V/фи-квадрат; критерий Макнемара, точный критерий Фишера (2×2 Tables: Xi/V/Phi, McNemar, Fisher exact).

Пример 1.

Чтобы определить отношение телезрителей разного пола к телевизионной передаче опросили 60 человек: 35 мужчин и 25 женщин. Оказалось, что 25 мужчин одобряют, а 10 – не одобряют эту передачу. В то же время 16 женщин высказывают свое отрицательное отношение к передаче, а 9 – положительное. Требуется выяснить, зависит ли отношение к передаче от пола телезрителей.

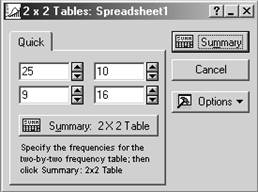Шаг 1. Выберите опцию 2×2 Tables (…), нажмите ОК и откройте диалоговое окно, в котором можно ввести частоты в таблицу 2×2 (состоящую из двух строк и двух столбцов) и вычислить различные статистики, позволяющие оценить зависимость между переменными, принимающими только два значения.

Шаг 2. Задайте исходные данные в таблице частот 2×2, затем нажмите кнопку Summary.

Шаг 3. Таблица результатов имеет вид:

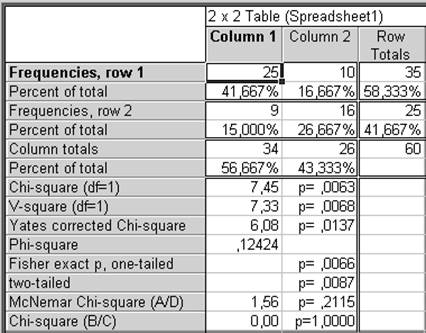
Частоты, строка 1

Процент от общего

Частоты, строка 2

Процент от общего

Сумма по столбцу

Процент от общего

хи-квадрат

V-квадрат

поправка Йетса

коэффициент фи-квадрат

точный критерий Фишера: односторонний

двусторонний

хи-квадрат Макнемара

хи-квадрат

Выводы. Р-значения для статистики хи-квадрат и статистики хи-квадрат, скорректированной по Йетсу, соответственно равны: 0,0063 и 0,0137. Таким образом, на уровне значимости α = 0,05 следует считать, что отношение к передаче зависит от пола.

Поправка Йетса обычно применяется, когда ячейки содержат только малые частоты и некоторые ожидаемые частоты становятся меньше 5 (или даже меньше 10).

В таблице результатов приводится мера связи между переменными