



Значимость частных коэффициентов корреляции проверяется по тем же критериям, что и парных. То есть находят наблюдаемое значение t-критерия:
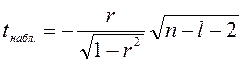 , где r – оценка частного коэффициента корреляции;
, где r – оценка частного коэффициента корреляции;
l – число фиксируемых факторов.
Проверяемый коэффициент корреляции считается значимым если tнабл. по модулю будет больше чем tкр, определяемое по таблице t-распределения для заданного α и v=n-l-2.
Множественный коэффициент корреляции характеризует тесноту связи между результативной переменной и независимыми. Он изменяется в пределах от 0 до 1 и рассчитывается по формуле:
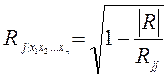 , где │R│ —
определитель корреляционной матрицы;
, где │R│ —
определитель корреляционной матрицы;
Rjj — алгебраическое дополнение jj-го элемента.
В случае двух объясняющих переменных формула для вычисления множественного коэффициента детерминации имеет вид:
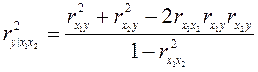 .
.
Квадрат множественного коэффициента корреляции называется множественным коэффициентом детерминации. Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных.
Значимость множественного коэффициента корреляции проверяется по F-критерию.
Наблюдаемое значение находится по формуле:
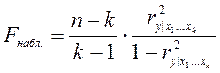 .
.
Множественный коэффициент корреляции считается значимым, т.е. имеет место статистическая зависимость между Y и остальными факторами X, если Fнабл. > Fкр. (α, k-1, n-k), где Fкр. определяется по таблице F-распределения.
Показателям тесноты связи можно дать качественную оценку на основе шкалы Чеддока:
|
Количественная мера тесноты связи (по модулю) |
Качественная характеристика силы связи |
|
0,1 – 0,3 0,3 – 0,5 0,5 – 0,7 0,7 – 0,9 0,9 – 0,99 |
слабая умеренная заметная высокая весьма высокая |
Заметим, что функциональная связь возникает при значении равном 1, а отсутствие связи — 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50%. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.
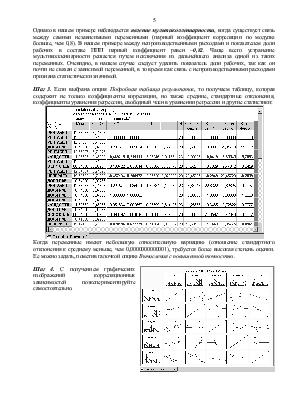
Основные этапы проведения корреляционного анализа в системе рассмотрим на данных Примера 1. Исходные данные представляют собой результаты наблюдений за деятельностью 23 предприятий одной из отраслей промышленности.
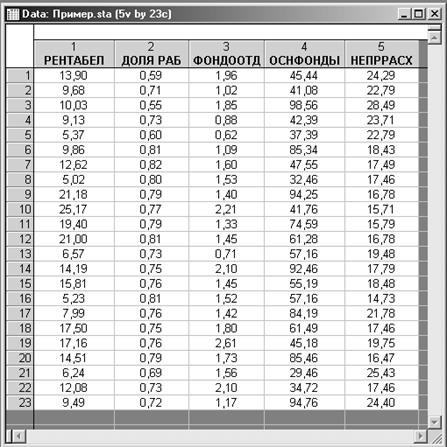
Графы таблицы содержат следующие показатели:
РЕНТАБЕЛ – рентабельность, %;
ДОЛЯ РАБ – удельный вес рабочих в составе ППП, ед.;
ФОНДООТД – фондоотдача, ед.;
ОСНФОНДЫ – среднегодовая стоимость основных производственных фондов, млн. руб.;
НЕПРРАСХ – непроизводственные расходы, тыс. руб.
Требуется исследовать зависимость рентабельности от других показателей.
Предположим, что рассматриваемые признаки в генеральной совокупности подчиняются нормальному закону распределения, а данные наблюдений представляют собой выборку из этой совокупности.
 Шаг 1.
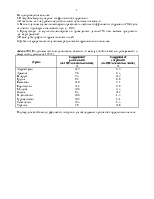
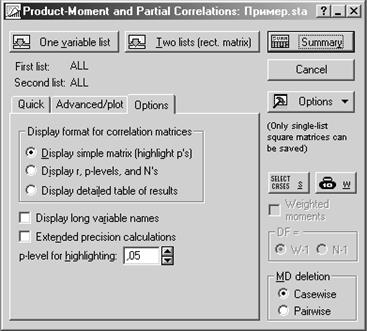
Вычислим парные коэффициенты корреляции между всеми переменными (Basic Statistics and Tables / Correlation matrices). Обратите внимание
на закладку Options (Опции) в появившемся диалоговом окне.
Шаг 1.
Вычислим парные коэффициенты корреляции между всеми переменными (Basic Statistics and Tables / Correlation matrices). Обратите внимание
на закладку Options (Опции) в появившемся диалоговом окне.
Кнопки:
один список (квадратная) / два списка (прямоугольная)
отображать простую матрицу
отображать уровень значимости, количество и r
отображать подробную таблицу результатов
отображать длинные имена переменных
вычисления с повышенной точностью
уровень значимости (p-level)
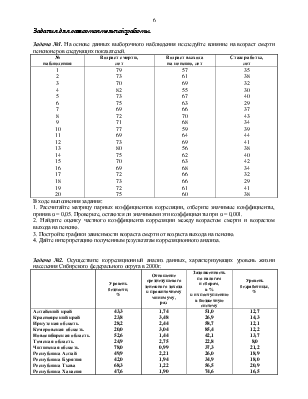
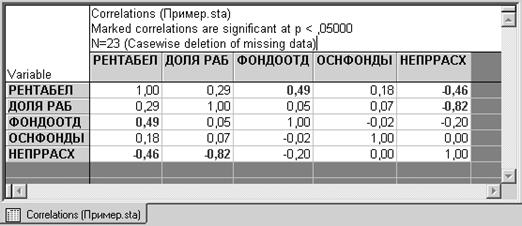 Шаг 2. В нашем
примере показатель рентабельности оказался наиболее связан с показателями
(выделены красным цветом):
Шаг 2. В нашем
примере показатель рентабельности оказался наиболее связан с показателями
(выделены красным цветом):
фондоотдача (связь прямая)
и непроизводственные расходы (обратная связь).
При дальнейшем построении уравнения регрессии следует ограничиться именно этими показателями как наиболее информативными.
Однако в нашем примере наблюдается явление мультиколлениарности, когда существует связь между самими независимыми переменными (парный коэффициент корреляции по модулю больше, чем 0,8). В нашем примере между непроизводственными расходами и показателем доли рабочих в составе ППП парный коэффициент равен –0,82. Чаще всего устранение мультиколлениарности решается путем исключения из дальнейшего анализа одной из таких переменных. Очевидно, в нашем случае следует удалить показатель доли рабочих
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.