основе данной в варианте формулы на указанном интервале значений аргумента получить ряд данных из 100 значений, выбрать соответствующий шаг дискретизации. Найти максимальное значение полученного ряда и ввести в значения ряда случайную составляющую, которая по модулю не превышает 5% от найденного максимального значения ряда. Построить график исходного ряда.
2. Произвести сглаживание исходного ряда методом скользящего среднего для 3-х и 5-ти точек в прямом и обратном порядке, а так же экспоненциальное сглаживание. Для каждого сглаживания построить график исходного и сглаженного ряда, выбрать один из перечисленных методов сглаживания, сделать вывод.
3. На основе сглаженного ряда данных произвести полиноминальную аппроксимацию, выбрать степень полинома соответствующую виду сглаженного ряда. На заданном интервале значений получить минимум и максимум полученной функции аппроксимации. Исходя из полученных результатов, подобрать точность коэффициентов полинома. Построить график функции аппроксимации и сглаженного ряда, сделать вывод.
4. Разбить сглаженный ряд данных на два рада данных (по 50 значений) – чётный и нечётный (по порядку следования значений). На основе чётного и нечётного ряда получить ряды по 100 значений путём вставки недостающих элементов как среднего арифметического между соседними элементами ряда. Построить графики чётного и нечётного ряда.
5. Произвести аппроксимацию чётного и нечётного ряда полиномом того же порядка, что и у полинома аппроксимации исходного сглаженного ряда. Построить графики аппроксимации чётного и нечётного ряда.
6. Рассчитать относительное отклонение коэффициентов полинома аппроксимации чётного и нечётного исходного ряда от коэффициентов полинома аппроксимации сглаженного ряда. Получить среднее отклонение коэффициентов, если оно укладывается в диапазон ±5%, то ряд однородный. Сделать вывод об однородности ряда.
Варианты заданий:
X1=100-3t; X2=0,5t2;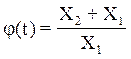
; tÎ[1;35]
Выберем шаг дискретизации и составим ряд.
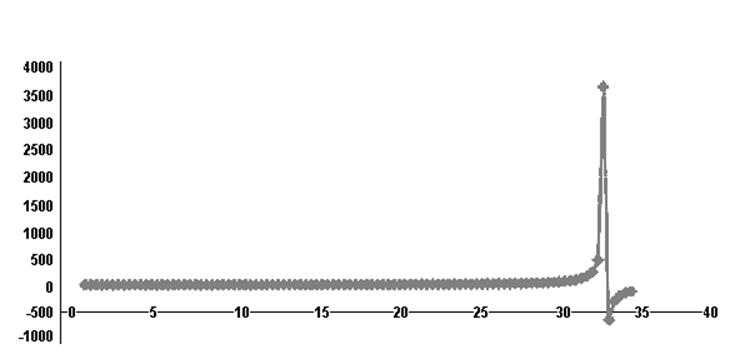
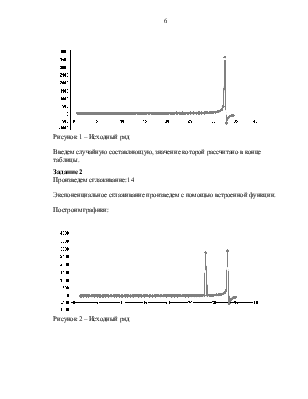
Рисунок 1 – Исходный ряд
Введем случайную составляющую, значение которой рассчитано в конце таблицы.
Произведем сглаживание:14
Экспоненциальное сглаживание произведем с помощью встроенной функции.
Построим графики:
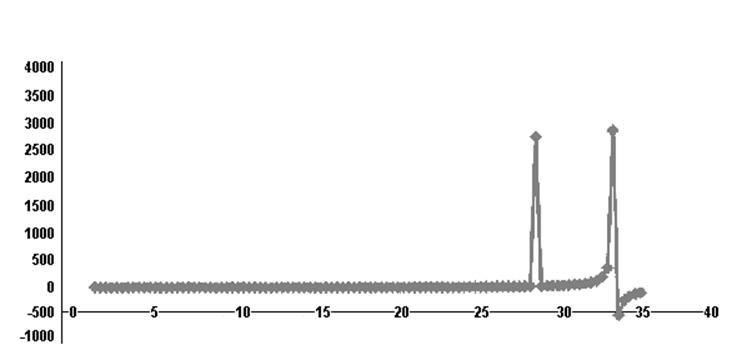
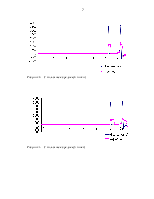
Рисунок 2 – Исходный ряд
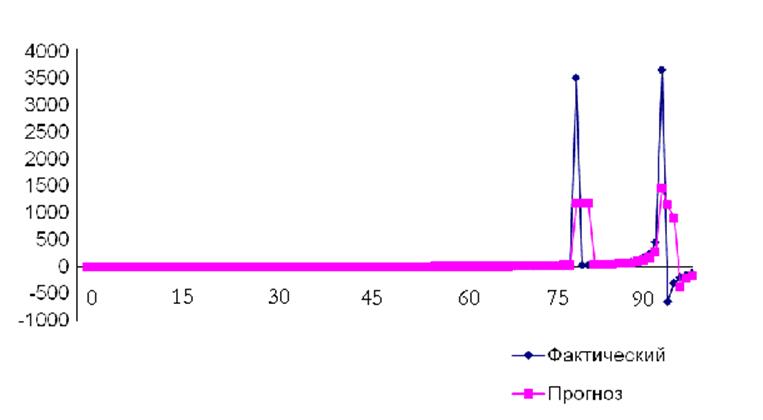
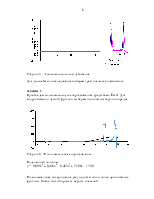
Рисунок 3 – Скользящее среднее(3 точки)
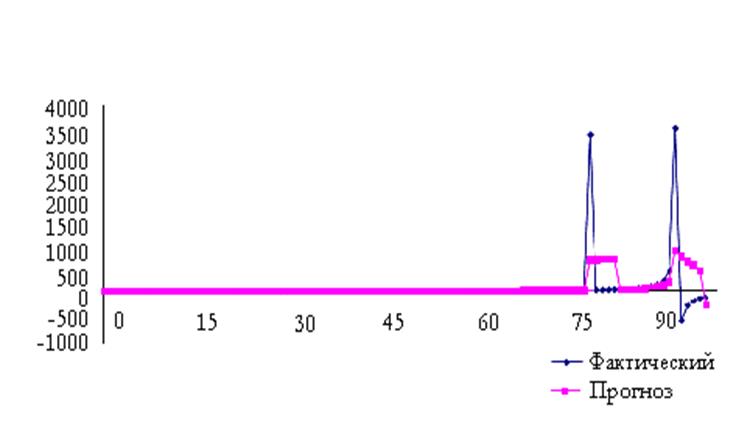
Рисунок 4 – Скользящее среднее(5 точек)
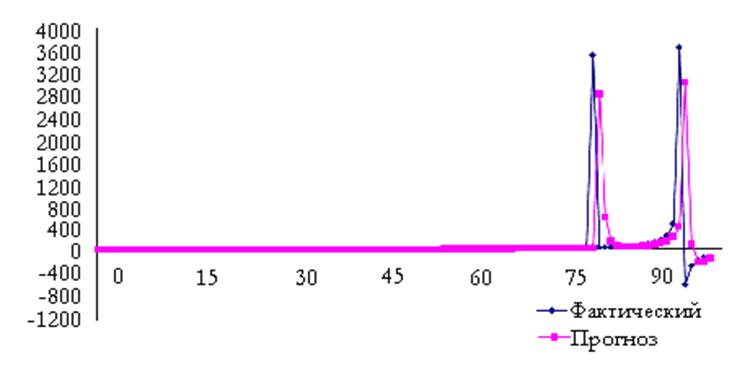
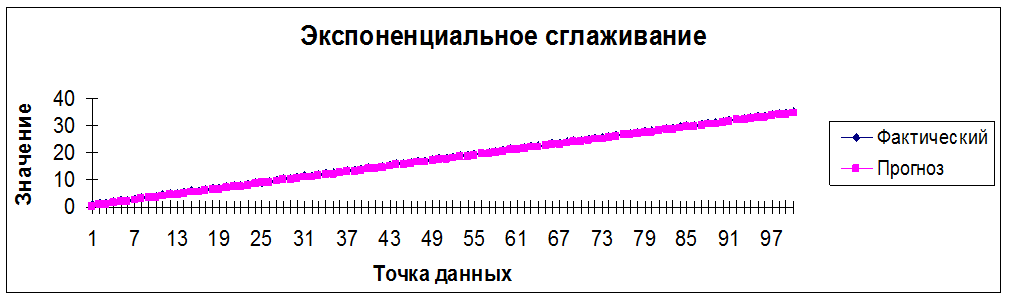
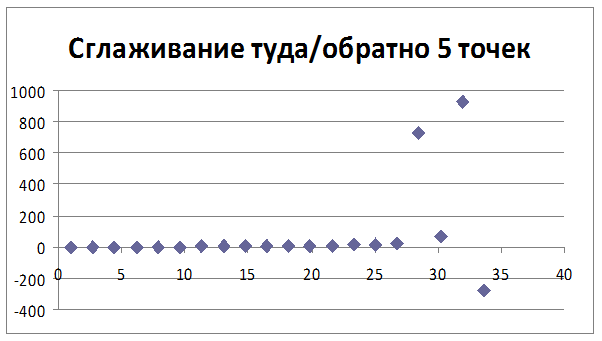
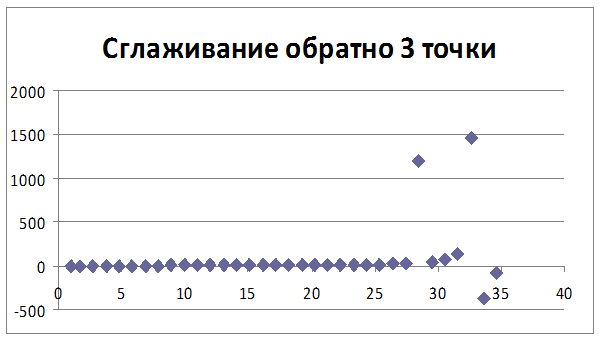
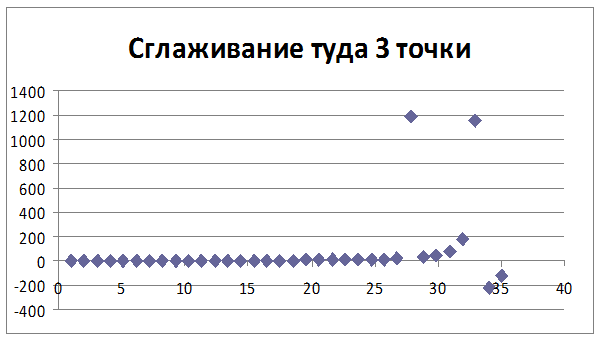
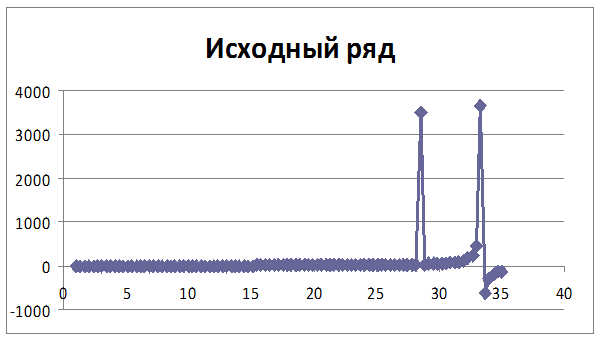
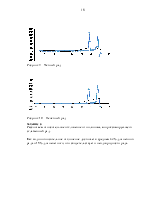
Рисунок 5 – Экспоненциальное сглаживание
Для дальнейшего исследования выберем трехточечное сглаживание.
Произведем полиномиальную аппроксимацию средствами Excel. Для аппроксимации данной функции выберем полином четвертого порядка.
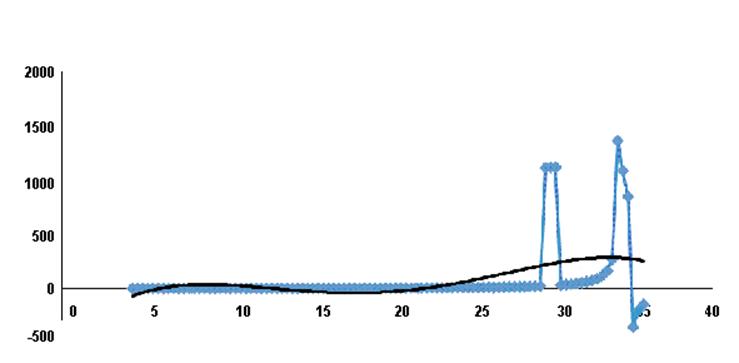
Рисунок 6 – Полиномиальная аппроксимация
Полученный полином:
y = -0,005x4 + 0,428x3 – 9,485x2 + 71,96x – 135,0
Полиномиальная интерполяция дает недостаточно точное приближение функции. Очень низкий процент верных значений.
Составим четный и нечетный ряды на основе выбранного сглаженного ряда.
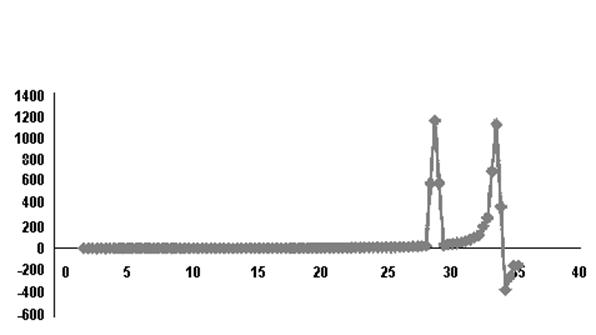
Рисунок 7 – Чётный ряд
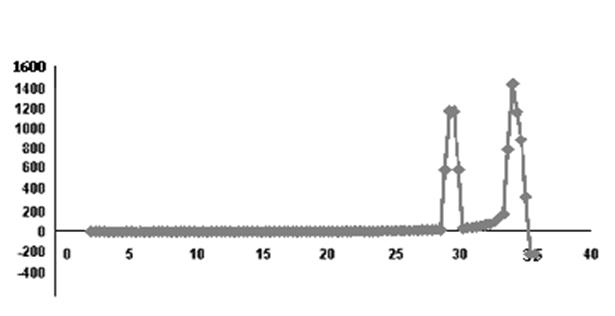
Рисунок 8 – Нечётный ряд
Видим, что данные, полученные таким способом, дают разный результат.
Аппроксимируем полученные ряды полиномом четвертого порядка.
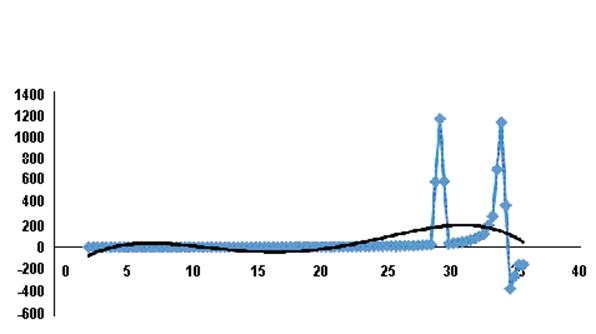
Рисунок 9 – Чётный ряд
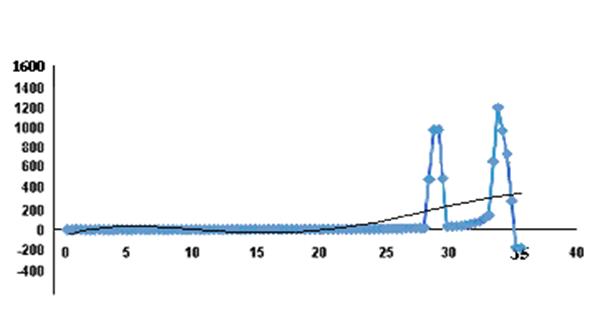
Рисунок 10 – Нечётный ряд
Рассчитаем относительное отклонение от полинома, аппроксимирующего сглаженный ряд.
Как видно относительное отклонение достигает в среднем 32% для четного ряда и 18% для нечетного, что свидетельствует о неоднородности ряда.
Вариант 7
Цель: освоить основные математические операции, выполнение которых
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.