Анализ выживаемости в системе Statistica. Введение в анализ выживаемости

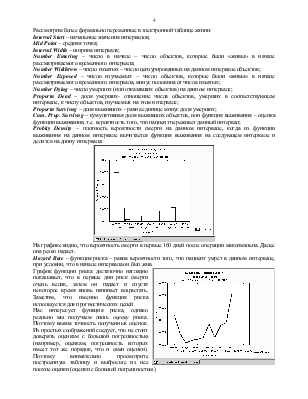
Формально S(t) = P{ x ≥ t }, где x – случайная величина, описывающая время жизни после операции. Заметьте, что функция выживания является убывающей функцией, равной 1 при t=0, и обращающейся в 0 при больших значениях t.

Если все наблюдения являются полными, то оценка S(t) строится легко: мы просто подсчитываем количество пациентов, проживших t дней после операции, и делим их на общее число пациентов. Наличие неполных наблюдений усложняет ситуации.

Оказывается, что для цензурированных наблюдений функцию выживания можно оценить непосредственно, не используя таблицу времени жизни. Такой метод впервые предложил Каплан и Мейер в 1958 году.

Представьте, что вы имеете файл, в котором записаны в хронологическом порядке отдельные события. Тогда имеет место следующая оценка функции выживания:

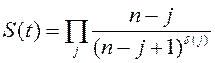
В этом выражении S(t) – это оценка функции выживания, n – общее число событий (объем выборки), j – порядковый (хронологический) номер отдельного события; δ( j ) равно 1, если j-ое событие означает отказ (смерть), и δ( j ) равно 0, если j-ое событие означает потерю наблюдения (индикатор цензурирования); П означает произведение по всем наблюдениям j, завершившимся к моменту t. Данная оценка функции выживания состоит из произведения нескольких сомножителей, поэтому она также называется множественной оценкой. Рассмотрим файл данных, что и для таблиц времен жизни. Принцип построения таблицы тот же, что и в анализе выживаемости и времен отказа. Оценка Каплана-Мейера функции выживания, построенная по этим данным, показана в следующей таблице.

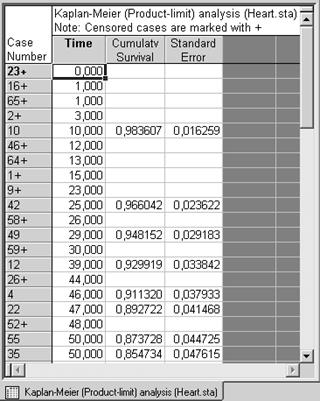
Из таблицы видно, например, что вероятность того, что пациент проживет больше 25 дней, равна 0,966; вероятность того, что пациент проживет больше 39 дней, равна 0,9299 и т.д. В первом столбце таблицы показаны номера наблюдений, для которых в данный момент времени произошло некоторое событие, знак «+» означает, что пациент цензурирован (выписан).

Обратите внимание на ошибки оценок (последняя колонка). Стандартная ошибка функции выживания достаточно мала (сравните с ошибками для таблиц времен жизни).

График функции выживания выглядит следующим образом:

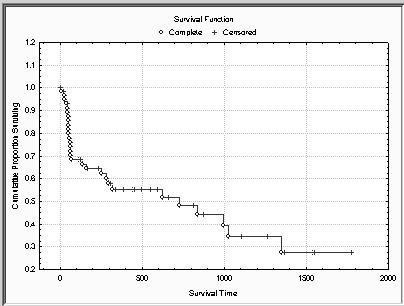
Отметим, что для удобства интерпретации на графике полные наблюдения помечены точками, неполные наблюдения отмечены крестиками.

Преимущество метода Каплана-Мейера (по сравнению с методом таблиц жизни) состоит в том, что оценки не зависят от разбиения времени жизни на интервалы.

Шаг 10. Интересно сравнить времена жизни пациентов в различных группах (например, в группах мужчины и женщины). В нашем случае сравним показатели для различных госпиталей, где сделана операция.

Если количество групп – две, то используется диалог Сравнение двух выборок.

В нашем случае количество групп больше двух, поэтому запустим диалог Сравнение нескольких выборок.

Окно для задания исходных данных такое же, как и в предыдущих модулях. Различие состоит в том, что необходимо задать группирующую переменную (в нашем случае это HOSPITAL) и соответствующие коды для неё (для нашего примера по умолчанию – это названия трех госпиталей, где сделана операция: HILLVIEW, ST_AND, BINER; можно их перекодировать в 1, 2, 3).

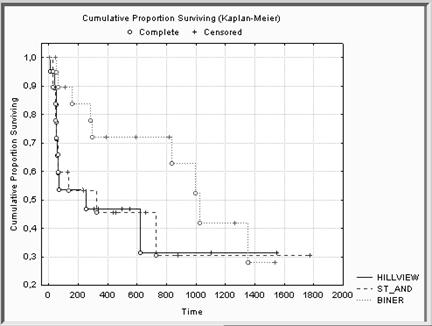
На полученном графике хорошо видно, что кумулятивная доля выживших в госпитале BINER выше, чем в двух других.

Отметим, что важно проверить доли цензурированных наблюдений в каждой