
































Билет 1. Определители второго порядка
и их свойства Билет 2. Определители третьего порядка
и их свойства Билет 3. Векторы. Основные
определения.
Билет 4.
Действия над векторами. Билет 5. Разложение вектора по
базису
Билет 6. Скалярное
произведение векторов, свойства, применение Билет 7. Линейная
зависимость и независимость векторов Билет 8. Деление отрезка в данном
отношении Билет 9. Векторное произведение
векторов, свойства, применение Билет 10. Смешанное произведение
векторов, свойства, применение Билет 11. Двойное векторное
произведение Билет 12. Преобразование координат
(параллельный перенос и поворот осей) Билет 14. Нормальное уравнение прямой Билет 15. Уравнение прямой проходящей через заданную точку, через две точки, общее уравнение, Билет 16. Особые случаи расположения
прямой на плоскости Билет 17. Плоскость. Общее
уравнение, в отрезках на осях, уравнение плоскости проходящей через три точки Билет 18. Особые случаи расположения
плоскости Билет 19. Расстояние от точки до
прямой Билет 20. Угол между двумя прямыми Билет 22.
Расстояние от точки до плоскости Билет 23.
Уравнение прямой в пространстве, векторное и каноническое уравнение прямой Билет 24.
Угол между прямыми в пространстве, между прямой и плоскостью Билет
25. Условия
параллельности и перпендикулярности прямых, условия параллельности и
перпендикулярности прямой и плоскости. Билет 26. Кривые второго
порядка. Окружность.
Элипс.
Билет 27. Гипербола Билет 28. Парабола Билет 29. Цилиндрические
поверхности Билет
30. Конические поверхности Билет 31.
Поверхности вращения. Элипсоид вращения. Билет 32. Эллиптический
параболоид Билет 33. Однополостный
гиперболоид Билет 34. Двуполостный
гиперболои
Билет
35. Гиперболический
парабалоид
Билет 36. Комплексные числа, основные понятия
Билет
37. Действия
над комплексными числами Билет
38. Показательная форма комплексного числа Билет 37. Действия над
комплексными
числами
Билет 39. Определители n-ого порядка. Правило Крамера. Билет 40. Матрицы. Основные понятия и определения Билет 42. Система линейных уравнений. Теорема Кронекера-Капелли Билет
41. Действия над матрицамиБилет 43. Однородные системы уравнений. Матричный
метод решения. Билет
44. Метод Гаусса Билет 45. Множество
вещественных чисел и их свойств Билет
46. Предел последовательности Билет
47. Верхние и нижние грани множеств Билет
48. Частичный предел Билет
49. Теорема о единственности предела числовой последовательности Билет 50. Второй
замечательный предел Билет 51. Функция. Предел
функции Билет
52. Теорема о пределах функции Билет 53. Непрерывность функции Билет 54. Теорема о
непрерывности сложной функции Билет 55. Первая теорема Больцано-Коши Билет 56. Вторая теорема Больцано-Коши Билет 57. Теорема Вейерштрасса о наибольшем и наименьшем значении
функции Билет 58. Теорема
Вейерштрасса об ограниченности функции Билет 59. Равномерная
непрерывная функция Билет 60. Бесконечно
малые функции. Основные теоремы Билет 61. Сравнение бесконечно малых функций Билет 62. Основные
теоремы о пределах Билет 63. Эквивалентные
бесконечно малые, их свойства Билет 64. Производная
функции. Геометрическая интерпретация Билет 65. Производная от
сложной функции Билет 66. Логарифмическое
дифференцирование, производная неявно заданной функции Билет 67. Дифференциал
функции, связь производной Билет 68. Инвариантность
формы первого дифференциала Билет 69. Производные и
дифференциалы высших порядков Билет 70. Не инвариантность
формы дифференциала порядка выше первого Билет 71. Теорема Ферма
и лемма к теореме Ферма Билет 72. Теорема Ролля Билет
73. Теорема Лагранжа Билет 74. Теорема Коши Билет 75. Правило Лопиталя раскрытия
неопределенностей Билет 76. Исследование функций и построение графиков Билет 78. Неопределенный
интеграл. Геометрический смысл Билет
80. Теорема Безу Билет
81. Теорема о комплексных корнях многочлена Билет 82. Простейшие
дроби и их интегрирование Билет 83. Интегрирование
иррациональности Билет 84. Интегрирование
тригонометрических функций Билет 85. Основные свойства неопределенных
интегралов Билет 86. Теорема о
среднем для определенного
интеграла
Билет 87. Замена переменной в определенном интеграле Билет 88. Вычисление
площадей с помощью определенного интеграла Билет
89. Площадь в полярных координатах Билет 93. Площадь поверхности
вращения Билет 1. Определители второго порядка и их свойства Пусть задана таблица вида(матрица) A= Свойства определителя второго порядка:1)
Значение определителя не изменится, если поменять строки со
столбцами(транспонирование). Свойство означает равноправие строк и столбцов. 2) Если в определителе строка или столбец
содержит все нули, то и определитель равен нулю. 3) Если в определителе элементы одной
строки или столбца равны элементам другой, то такой определитель равен нулю. 4) Если строка или столбец содержит общий
множитель, то его можно вынести за знак определителя 5) Если поменять местами две строки или
два столбца, то знак определителя поменяется на противоположный 6) Если элементы одной строки или столбца
умножить на одно и то же число и добавить к элементам другой строки или
столбца, то значение определителя не изменится Билет 2. Определители третьего порядка и их свойства Определитель третьего порядка: Сокращенное обозначение выражения: Выражение через определители второго
порядка: Минором элемента определителя третьего
порядка называется определитель второго порядка, который получится, если в
исходном определителе вычеркнуть строку и столбец, содержащие данный элемент: Свойства: 1) Значение определителя не изменится,
если:- строки заменить на столбцы, такое действие называется транспонирование,
т.е. действия, выполняемые со строками, справедливы и для столбцов; - все элементы одной строки умножить на
какое-либо число и прибавить к соответствующим элементам другой строки. 2) Определитель меняет знак на
противоположный, если:- две каких-либо строки поменять местами. 3) Определитель равен нулю, если:- все
элементы какой-либо строки равны нулю;- соответствующие элементы каких-либо
двух строк равны; - соответствующие элементы каких-либо
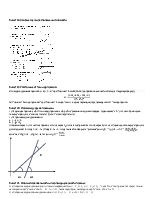
двух строк пропорциональны. Билет 3. Векторы. Основные определения. Вектор
- это направленный отрезок, то есть отрезок, имеющий длину и определенное
направление. Графически вектора изображаются в виде направленных отрезков
прямой определенной длины. Нулевой вектор – это любая точка
плоскости или пространства, начало и конец вектора совпадают, а его длина равна
нулю. Длина вектора
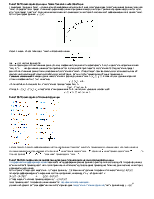
![]() Билет 21. Условие параллельности и перпендикулярности прямых
Билет 21. Условие параллельности и перпендикулярности прямых
![]() Билет 90.
Объем тела Билет
91. Объем тела вращения Билет
92. Длина дуги кривой
Билет 90.
Объем тела Билет
91. Объем тела вращения Билет
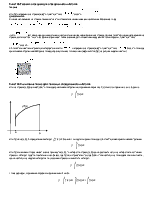
92. Длина дуги кривой![]() Билет 100.
Частное и полное приращение функции
Билет 100.
Частное и полное приращение функции![]() то определителем
второго порядка для данной матрицы будет формула вида
то определителем
второго порядка для данной матрицы будет формула вида ![]() .
.![]() . Следствие:
если элементы строки или столбца пропорциональны другой, то определитель будет
равен нулю.
. Следствие:
если элементы строки или столбца пропорциональны другой, то определитель будет
равен нулю.![]()
![]()
![]() .
.![]() .
.![]() .
.![]()
![]() ;
;![]() в прямоугольных декартовых координатах равна
в прямоугольных декартовых координатах равна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.