Теория игр. Решение в смешанных стратегиях

Лабораторная работа 3

Тема “Теория игр. Решение в смешанных стратегиях”

Порядок работы

1.  Выбрать задачу в соответствии со своим номером.

2.  Написать платежную матрицу, математическую модель прямой и двойственных вспомогательных задач, указав экономический смысл всех переменных.

3.  Подготовить данные в Exсel и провести расчет  задачи.

4.  Проанализировать полученный результат.

Образец

1.  Задача о выборе режима технологической линии

На технологическую линию поступает сырье с малым или большим количеством примеси. Линия может работать в четырех режимах. Доход предприятия от единицы продукции, изготовленной из сырья первого вида при различных режимах работы технологической линии составляет 1, 2, 5, 5 д.ед., из сырья второго вида – 2. 5, 3, 2 д.ед, третьего вида – 4, 1, 2, 3 д.ед. В каких режимах и сколько процентов времени должна работать технологическая линия, чтобы доход от выпускаемой продукции был максимален.

Рассматриваемая задача может быть сведена к игровой модели, в которой игра предприятия А против поставщика сырья задана платежной матрицей

Находим нижнюю (a = 2) и верхнюю (b = 4) цену игры. Игра не имеет решения в чистых стратегиях, следовательно, будем рассматривать смешанные стратегии (p₁, p_2, p₃, p₄) , где p_i – вероятности того, что система находится в i-ом режиме. Цена игры a £ n £ b.

Строим задачу линейного программирования, с помощью решения которой находятся p_i.

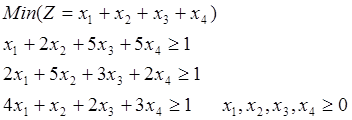
Тогда n = 1/Z – гарантированный выигрыш (прибыль предприятия от ед. сырья), p_i = x_i*n - вероятность того, что система работает в i-ом технологическом режиме.

Решение задачи, двойственной к указанной, дает вероятности распределения сырья по видам, при котором и получается гарантированный выигрыш. Во всех других случаях (соотношениях сырья по видам) выигрыш (прибыль предприятия) будет больше или равен указанному.

3. Заполним расчетные таблицы в Excel.

В ячейки B4-D7 вводим коэффициенты платежной матрицы. В ячейках Е4-Е7 надоим минимальный выигрыш в случае каждой стратегии, для чего в ячейку Е4 вводим формулу   =МИН(В4:D4), которую копируем в ячейки Е5-Е7. Аналогично в ячейках B8-D8 находим максимальные элементы в столбцах, для чего в ячейку В8 вводим формулу =МАКС(В4:В7), которую копируем в ячейки С8 - D8.

Так как нижняя цена игры не равна верхней, формируем вспомогательную задачу линейного программирования.

Ячейки В11-Е11 отводятся для переменных задачи, В12-Е14 – матрица коэффициентов ограничений, выделим ячейки В12-Е14 вводим формулу =ТРАНСП(В4:D7), после чего, поставив курсор в конец формулы(!!!), нажимаем одновременно клавиши Ctrl+Shift+Enter.

Вычисляем левые части ограничений, для чего в ячейку F12 введем формулу =СУММПРОИЗВ(В12:Е12;В$11:Е$11), которую скопируем в ячейки F13-F14. Целевая функция вычисляется в ячейке F11 = СУММ(В11:Е11).

3. Поставив курсор в ячейку F11, выберем пункт меню СЕРВИС-ПОИСК РЕШЕНИЯ. Заполняем входные данные

целевая функция F11

минимум

изменяемые ячейки В11-Е11

ограничения В11:Е11 >= 0   

F12:F14 >= 1

Выполнить      Параметры – Линейная модель OK Выполнить Устойчивость ОК

Если все сделано правильно, появится сообщение о том, что найдено оптимальное решение. Теневые цены следует скопировать с листа “Отчет по устойчивости” в ячейки G12-G14.   

Проведем дополнительные расчеты. Вычислить p_i = x_i/Z^* в ячейках В10-Е10, q_i = y_i/Z^* в ячейках G10-G14.

Конечная таблица приведена ниже.

3. Анализ результата

Расчет показывает, что предприятию следует использовать возможные четыре технологических режима в таких пропорциях: 34,62% : :26,92% : 0,00% : 38,46%, при этом предприятие может получить не менее 2,81 д.ед прибыли от единицы продукции вне зависимости от сорта сырья.