Расчет оптимального плана производства

Лабораторная работа 1

Тема “Расчет оптимального плана производства”

Порядок работы

1.  Выбрать задачу в соответствии со своим номером.

2.  Написать математическую модель прямой и двойственной задачи, указав экономический смысл всех переменных.

3.  Подготовить данные в Exel.

4.  Провести расчет прямой и двойственной задачи.

5.  Проанализировать полученный результат.

Образец

1. Задача. Автозавод выпускает 2 модели: "Каприз" и (более дешевую) "Фиаско". На заводе работает 1000 неквалифицированных и 800 квалифицированных рабочих, каждому из которых оплачивается 40 час/нед. Для  изготовления модели "Каприз" требуется 30 час неквалифицированного и 50 час квалифицированного труда; для "Фиаско" - 40 час неквалифицированного и 20 час квалифицированного труда.

Каждая модель "Фиаско" требует затрат в размере 500$ на сырье и комплектующие изделия, тогда как каждая модель "Каприз" требует затрат 1500$; суммарные затраты не должны превосходить 900000$ в неделю. Рабочие, осуществляющие доставку, работают по 5 дней в неделю и могут забрать с завода не более 210 машин в день.

Каждая модель "Каприз" приносит фирме 1000 дол прибыли, а каждая модель "Фиаско" - 500 дол прибыли.

Требуется ответить на вопросы

Какой объем выпуска  каждой модели Вы бы порекомендовали?

Что бы Вы порекомендовали для повышения прибыли фирмы?

2. Математическая модель прямой задачи

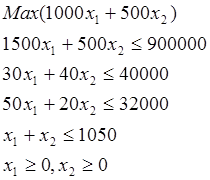
Математическая модель двойственной задачи

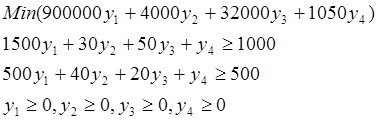
3. Создадим таблицу в Exel для расчета аналогичной задачи для случая 5 основных переменных при 5 ограничениях на них.

В ячейки В7:С7 введем коэффициенты целевой функции, в ячейки В10:С13 введем коэффициенты системы ограничений задачи, в ячейки I10:I13 – правые части системы ограничений. Ячейки В4:С4 используются для искомых значений алана производства. Начальные значения в них можно не вводить.

После этого введем формулы: в ячейку G7 (значение целевой функции) – =СУММПРОИЗВ(B4:F4;B7:F7), в ячейку I7 (значение целевой функции двойственной задачи)- =СУММПРОИЗВ(J10:J15;I10:I15). В ячейкуB8 введем формулу =СУММПРОИЗВ($J10:$J15;B10:B15), которую скопируем в ячейки С8:F8, в ячейку G10 введем формулу  =СУММПРОИЗВ(B$4:F$4;B10:F10), которую скопируем в ячейки G11:G13.

4. Поставив курсор в ячейкуG7, выберем пункт меню СЕРВИС-ПОИСК РЕШЕНИЯ. Заполняем входные данные

целевая функция G7

максимум

изменяемые ячейки B4:F4

ограничения B4:F4 >= 0   

G10:G15 <= I10:I15

Параметры  Линейность   OK     Выполнить.

Если все сделано правильно, появится сообщение о том, что найдено оптимальное решение, после этого выбираем тип отчета    Устойчивость    OK.

Переходим на лист “Устойчивость”, копируем ячейки Е18:Е23, возвращаемся в текущий лист и вставляем скопированные ячейки в J10:J15. После этого возвращаемся и удаляем лист “Устойчивость”.

В итоге получаем

5. Анализ результата

План производства 366,667 автомобилей “Каприз” и 683,333 “Фиаско” (Не целые значения переменных рассматриваем как не полностью готовый автомобиль), общая прибыль 708333,3$.

При этом не полностью истрачены финансы (остаток 8333,3$), неквалифицированная рабочая сила, квалифицированная рабочая сила полностью задействована, все автомобили вывезены.

Отличны от 0 двойственные оценки полностью истраченных ресурсов, оставшиеся ресурсы имеют нулевые двойственные оценки, целевая функция двойственной задачи (суммарная оценка наличных ресурсов) равна суммарной прибыли.

Суммарная стоимость ресурсов по каждому автомобилю равна его прибыли.

Для увеличения прибыли фирме необходимо увеличить количество квалифицированной рабочей силы, каждый дополнительный час принесет прибыль равную 16,7$ и увеличить объем отправки автомобилей с завода.

Вопросы по лабораторной работе № 1

1.  Пояснить понятия: план выпуска продукции, оптимального плана производства, целевой функции, ресурса, дефицитный ресурс, избыточный ресурс.

2.  Общая задача ЛП, канонический вид задача ЛП, стандартный вид задачи ЛП.

3.  Какие переменные называются базисными, какие свободные. Показать их в модели, на листе Excel.

4.  Сформулировать 1,2,3 теоремы двойственности, критерий Канторовича. Показать их справедливость на примере решения задачи.

5.  Пояснить экономический смысл всех переменных. Какова их размерность?

6.  Что показывают двойственные оценки. Их размерность.

7.  Как проверить правильность решения задачи на листе Excel