Контрольные вопросы по математике
для специальностей ФК, БА, МЭ
Линейная алгебра 4/4
1. Векторное пространство Rn, сложение и умножение на число, 8 свойств. Общее понятие векторного пространства (8 аксиом). Скалярное произведение и модуль вектора в Rn. Ортогональность и коллинеарность.
2. Линейные комбинации и зависимость (равнозначные определения). Базис и размерность векторного пространства.
3. Линейные отображения и матрицы. Действия над отображениями и матрицами. Умножение матриц. Запись линейного отображения в матричном виде. Единичная матрица.
4. Определители второго и третьего порядков. Правило Саррюса. Свойства определителей. Миноры и адъюнкты. Разложение определителя по строке и столбцу.
5. Определители n-го порядка. Критерий равенства определителя нулю. Обратная матрица.
6. Система n линейных уравнений с n неизвестными. Запись и решение в матричном виде. Формулы Крамера.
7. Миноры прямоугольной матрицы, свойства миноров. Ранг прямоугольной матрицы (равнозначные определения).
8. Система m линейных уравнений с n неизвестными. Метод Гаусса. Матрица и расширенная матрица системы уравнений. Теорема Кронекера – Капелли.
Аналитическая геометрия 5/5
9. Прямоугольная система координат в плоскости. Направленный отрезок, его проекции на оси координат, длина и направление. Уравнение окружности, отыскание центра и радиуса.
10. Прямая в плоскости. Угловой коэффициент. Уравнения прямой с заданным угловым коэффициентом, проходящей через две точки, уравнение в отрезках.
11. Угол между прямыми в плоскости. Признаки параллельности и перпендикулярности прямых.
12. Векторное пространство R2. Отождествление вектора с направленными отрезками, равенство длин и одинаковая направленность отрезков. Геометрическое отображение линейных операций.
13. Скалярное произведение векторов в R2, его геометрический смысл. Угол между векторами, косинус и синус угла. Признаки ортогональности и коллинеарности векторов. Проекция вектора на вектор.
14. Общее уравнение прямой в плоскости, геометрический смысл его коэффициентов. Нормированное уравнение прямой. Геометрический смысл его левой части (расстояние от точки до прямой).
15. Прямоугольная система координат в пространстве. Направленный отрезок, его проекции, длина и направление. Уравнение сферы, отыскание центра и радиуса.
16. Общее уравнение плоскости в пространстве, геометрический смысл коэффициентов. Нормированное уравнение плоскости. Геометрический смысл его левой части.
17. Уравнения прямой в пространстве, направляющий вектор. Углы между прямыми и плоскостями. Взаимное расположение плоскостей и прямых в пространстве.
18. Кривые второго порядка. Эллипс, гипербола, парабола. Канонические уравнения. Директриса и эксцентриситет. Асимптоты параболы.
Введение в анализ, пределы 3/3
19. Промежутки числовой оси. Ограниченные множества, существование для них точной верхней и нижней границ (sup, inf). Собственные и несобственные точки. Окрестности точек. Вольное и строгое определение предела функции.
20. Ограниченность функции, имеющей предел. Бесконечно малые, их связь с функциями, имеющими предел. Теоремы о бесконечно малых и бесконечно больших.
21. Предел суммы, разности, произведения и частного.
22. Перенос строгого неравенства с предела на функцию. Предельный переход в неравенствах. Теорема о промежуточной функции. Первый замечательный предел.
23. Второй замечательный предел. Число е. Натуральные логарифмы. Функции, эквивалентные в точке. Список эквивалентных. Замена на эквивалентные при вычислении предела.
24. Функции, непрерывные в точке. Равнозначные определения непрерывности. Непрерывность суммы, разности, произведения, частного.
25. Непрерывность составной и обратной функций. Односторонняя непрерывность.
26. Класс элементарных функций, их непрерывность. Классификация точек разрыва функции.
27. Теорема о функциях, непрерывных на отрезке (Больцано – Коши, Вейерштрасса и Кантора).
Производная и дифференциал 5/5
28. Производная, её геометрический и механический смысл. Связь между дифференцируемостью и непрерывностью. Производная константы, показательной и логарифмической функций.
29. Производная степенной функции, синуса, косинуса.
30. Линейные свойства производной. Производная произведения и частного. Производная tgx, ctgx.
31. Производная составной и обратной функции. Производная обратных тригонометрических функций.
32. Производная функции, заданной параметрически. Список формул и правил дифференцирования. Уравнение касательной к графику функции.
33. Дифференциал, его геометрический смысл. Производная как отношение дифференциалов. Дифференциал составной функции, инвариантность формы дифференциала.
34. Дифференциал в приближенных вычислениях. Производные и дифференциалы высших порядков. Нарушение инвариантности.
35. Локальный максимум и минимум. Экстремум. Необходимый признак экстремума (теорема Ферма). Задачи отыскания наибольшего и наименьшего значения функции.
36. Теоремы Ролля и Лагранжа.
37. Критерии возрастания, убывания, константы. Достаточный признаки экстремума по первой производной.
38. Теорема Коши и следствия из неё, правило Лопиталя.
39. Формула Тейлора с остатком по Пеано. Достаточный признак экстремума по второй производной.
40. Формула Тейлора с остатком по Лагранжу. Ряд Тейлора, его сходимость, признаки сходимости. Разложение в ряд Тейлора функций еx, sin x, cos x, (1 + х)n.
41. Выпуклые вниз (вверх) функции. Критерии выпуклости.
42. Точки перегиба, необходимые и достаточные признаки. Асимптоты. Схема исследования и построения графика функции.
Первообразная и неопределенный интеграл (2/2)
43. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Замена переменной интегрирования. Список формул интегрирования элементарных функций.
44. Интегрирование по частям. Интегралы от простейших рациональных функций.
45. Понятие определенного интеграла. Линейные свойства. Суммы Дарбу. Признак существования.
46. Аддитивность. Интегрирование неравенств. Теорема о среднем.
47. Интеграл с переменным верхним пределом. Формула Ньютона - Лейбница.
48. Интегрирование по частям и замена переменной в определенном интеграле.
49. Приложения определенного интеграла в геометрии и экономике. Понятие несобственного интеграла.
Функции нескольких переменных (3/3)
50. Функция многих переменных как функция точки. Предел и непрерывность. Частные производные. Дифференцируемые функция и их дифференциал. Производные составных функций. Линии уровня и градиент функции Производная по направлению.
51. Формула Тейлора для функций многих переменных. Применение в приближенных вычислениях. Экстремум, необходимые и достаточные условия.
Дифференциальные уравнения (4/4)
52. Понятие дифференциального уравнения. Порядок уравнения. Частные и общее решения. Уравнения первого порядка (с разделяющимися переменными, линейные, Бернулли, однородные).
53. Начальные условия. Задача Коши. Теоремы существования и единственности решения для уравнений 1-го и 2-го порядка. Линейные уравнения 2-го порядка.
54. Структура общего решения линейного однородного уравнения. Критерий линейной независимости решений линейного однородного уравнения.
55. Уравнения с постоянными коэффициентами. Характеристическое уравнение. Общее решение в случае вещественных корней характеристического уравнения. Комплексные числа и функции. Формула Эйлера. Характеристическое уравнение с комплексными корнями.
56. Структура общего решения линейного неоднородного уравнения. Отыскание частного решения по виду правой части уравнения. Принцип наложения. Понятие о приближенных методах решения дифференциальных уравнений.
Числовые и функциональные ряды (3/3)
57. Числовой ряд, частичная сумма и сумма ряда, сходимость и расходимость ряда. Примеры. Признаки сходимости (сравнения, Даламбера, Коши, Лейбница). Абсолютная и условная сходимость. Функциональные ряды. Степенные и тригонометрические ряды.
1. Общий курс высшей математики для экономистов. Под редакцией Ермакова В. И. - М.: Инфра-М, 2001.
2. Сборник задач по высшей математике для экономистов. Под ред. Ермакова В. И. - М.: Инфра-М, 2001.
3. Высшая математика для экономистов. Под редакцией Кремера Н. Ш. - М.: ЮНИТИ, 1998.
4. Максимов Ю.Д. и др. Курс высшей математики для гуманитарных специальностей. - СПб: Спец. Лит-ра, 1999.
5. Красс М. С., Чупрынов Б. П. Основы математики и ее приложения в экономическом образовании. - М.: Дело, 2000.
6. Шипачев В. С. Высшая математика. - М.:ВШ, 1998.
РГЗ-1 Линейная алгебра и аналитическая геометрия, введение в анализ. 7 неделя
КР-1 Линейная алгебра, аналитическая геометрия, дифференциальное и интегральное исчисление. 8 неделя
РГЗ-2 Функции многих переменных и дифференциальные уравнения. 16 неделя
РГЗ-1 WE-BA-FC
Буква N замещается порядковым номером студента в журнале учебной группы.
1. Решить системы методом Гаусса и Крамера.
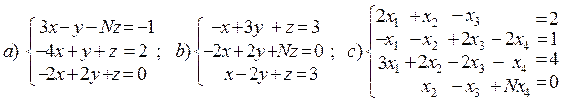
2.
Решить матричные
уравнения 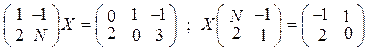
3. Составляют ли векторы u = (1, -1, -2), v.= (1; N; 0), w =(-1; 2; 4). базис в пространстве R3? Если подтвердится, то разложить вектор a = (3; 0; -1) по этому базису.
4. Дан треугольник ABC, A(3; N-3); B(-1; N), C(0; 3). Вычислить его площадь и высоту CE. Составить уравнение высоты CE.
5. Составить уравнения сторон треугольника АВС, если известна его вершина А(1; N) и две высоты 3х + 4у +1 = 0 и х + у ‑ N = 0. Вычислить площадь DABC.
6. Вычислить угол a) между векторами u = (2, -1, -2) и v.= (1; N; 0); b) между прямыми Nx – y =1, 4x – 3y = N. c) На первой из этих прямых найти точку, удалённую от второй прямой на расстоянии 1 единицы.
7.
На прямой ![]() найти точку, отстоящую от плоскости 2x+y-2z+N/2 = 0 на расстоянии N/6
единиц.
найти точку, отстоящую от плоскости 2x+y-2z+N/2 = 0 на расстоянии N/6
единиц.
8. Найти положение фокуса и директрисы a) параболы y =Nx2; b) эллипса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.