





Министерство образования Российской Федерации
Красноярский Государственный Технический Университет
Кафедра ТОТ

РАСЧЕТ НЕСТАЦИОНАРНОГО
НАГРЕВА ПАРАЛЛЕЛЕПИПЕДА
Выполнил:
студент группы Т83-1
Карцев П.В.
Проверил:
Ромащенко А.С.
Красноярск – 2005
Дано: b= 0,2 м
c= 3*a= 0,6 м
d= 2*а= 0,4 м
tЖ= 1000 0С
t0= 50 0C
τ= 1500 c
λ= 40 Вт/м*К
ρ=4 кг/м3
с0=4 Дж/кг*К
α=140 Вт/м2/К
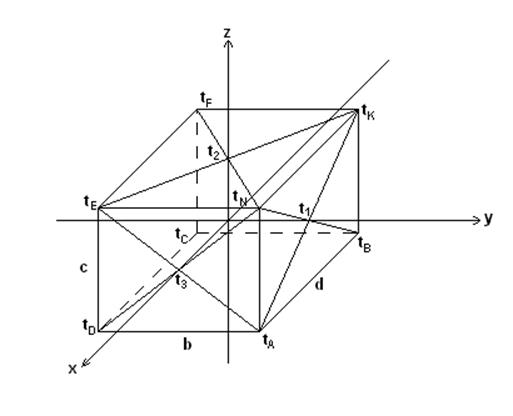
Найти: t1, t2, t3, t4, t5, t6
tA, tB, tC, tD, tE, tF, tK, tN, tЦ, Q
Рисунок:
Решение:
Данный параллелепипед образован пересечением трех неограниченных пластин, поэтому искомое распределение температур в данном параллелепипеде будет являться произведением температурных полей всех трех неограниченных пластин.
Запишем математическую постановку задачи:
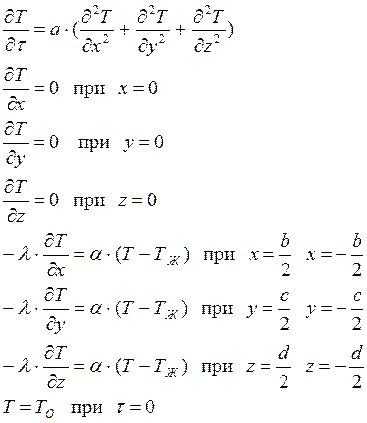
Расчитаем коэффициент температуропроводности:
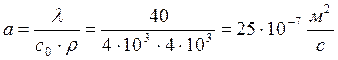
Введем и расчитаем следующие параметры:
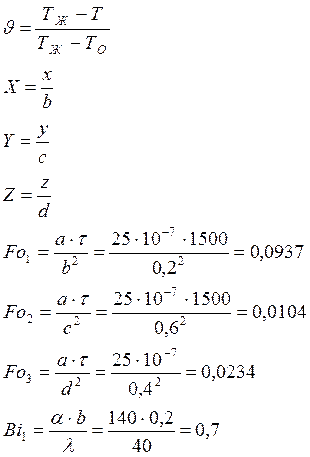
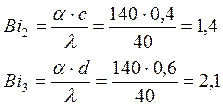
С помощью рассчитанных параметров приведем задачу к безразмерному виду, и
разобьем задачу на три самостоятельных, так как искомое распределение
температур в данном параллелепипеде является произведением температурных
полей трех неограниченных пластин (индекс 1 – для пластины толщиной b,
2 – для пластины толщиной с, 3 – для пластины толщиной d). Тогда:
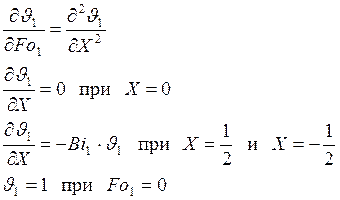
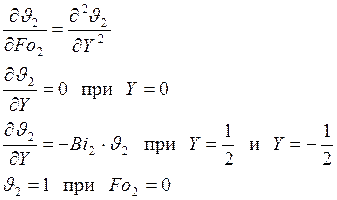
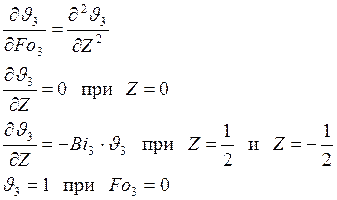
Решение этих задач будет иметь вид:
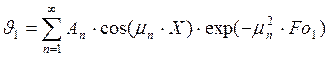
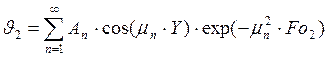
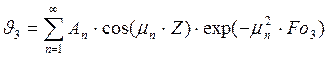
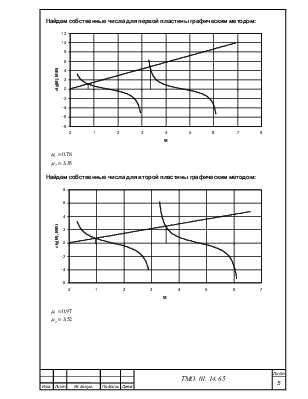
Найдем собственные числа для первой пластины графическим методом:
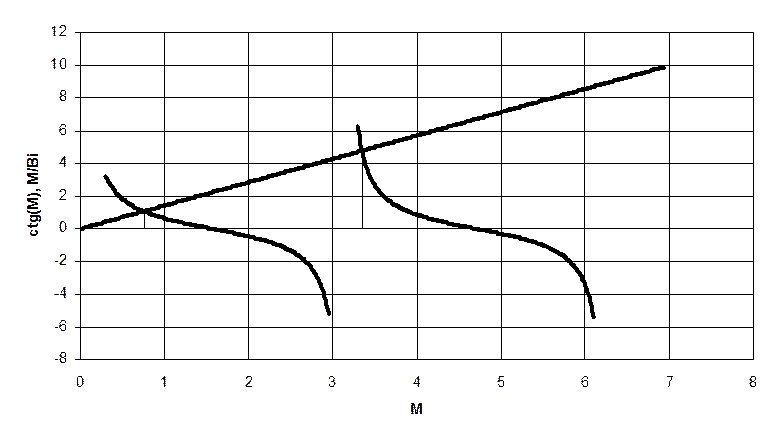
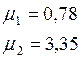
Найдем собственные числа для второй пластины графическим методом:
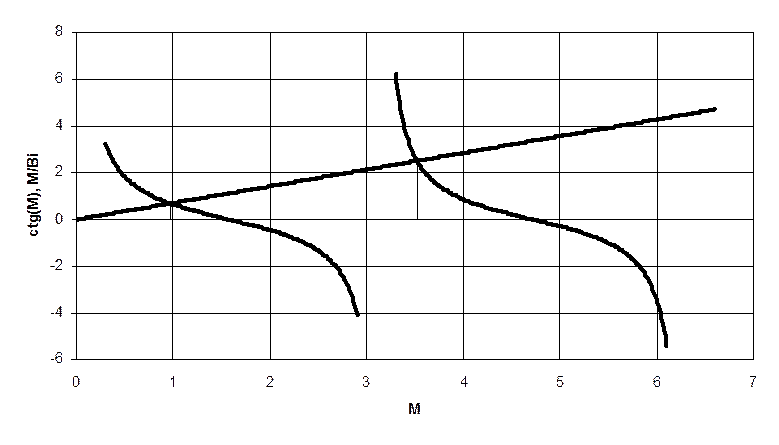
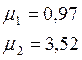
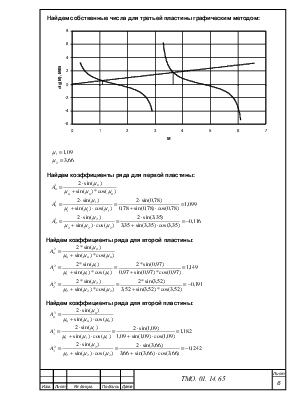
Найдем собственные числа для третьей пластины графическим методом:
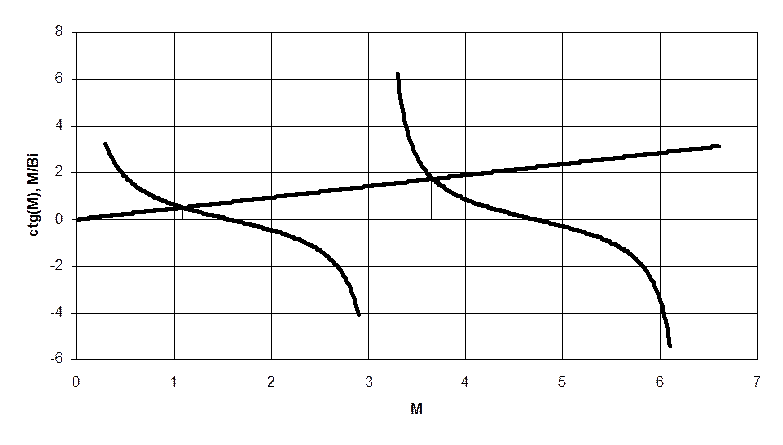
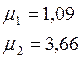
Найдем коэффициенты ряда для первой пластины:
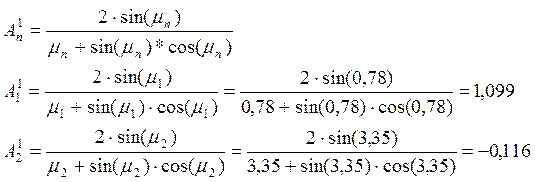
Найдем коэффициенты ряда для второй пластины:
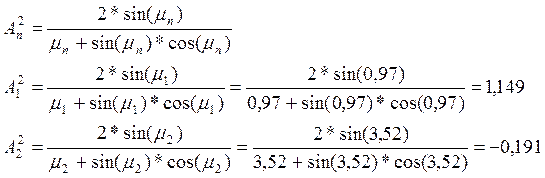
Найдем коэффициенты ряда для второй пластины:
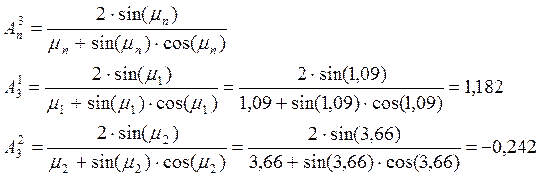
Найдем температуру центра параллелепипеда:
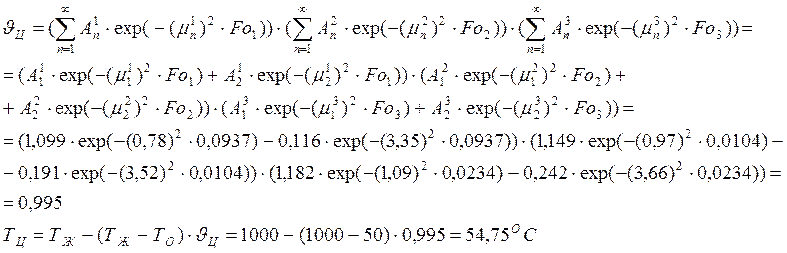
Найдем температуру точки 1:
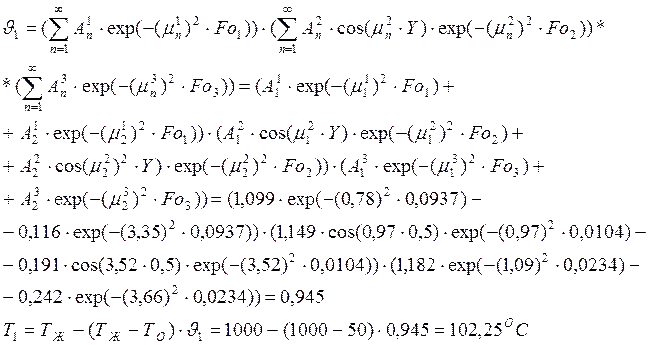
Найдем температуру точки 2:
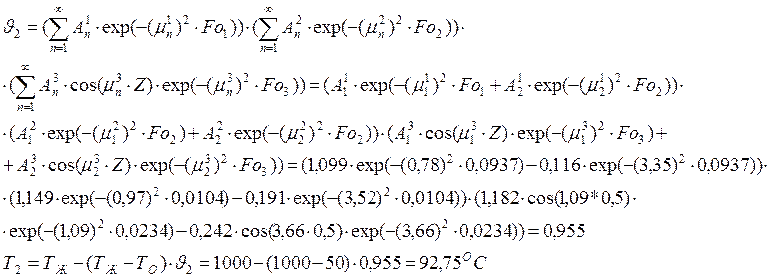
Найдем температуру точки 3:
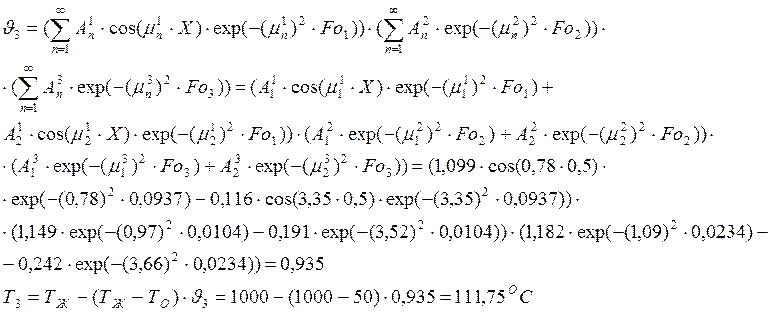
Найдем температуру точки А (температуры во всех вершинах будут одинаковы
в силу симметрии нагреваемого образца):
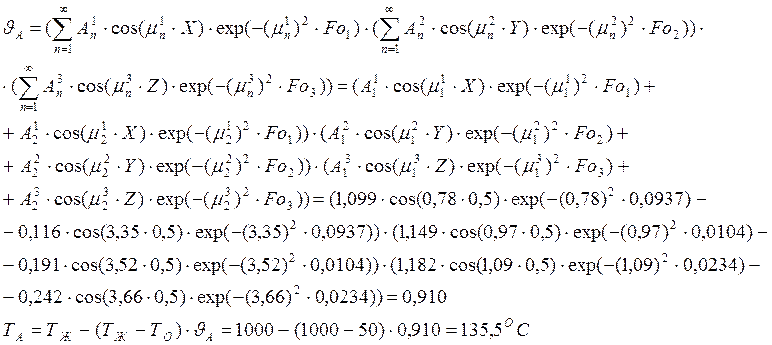
Найдем среднюю температуру параллелепипеда:
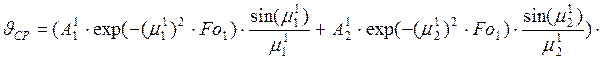
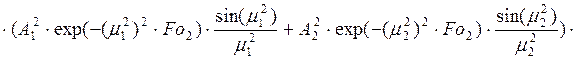
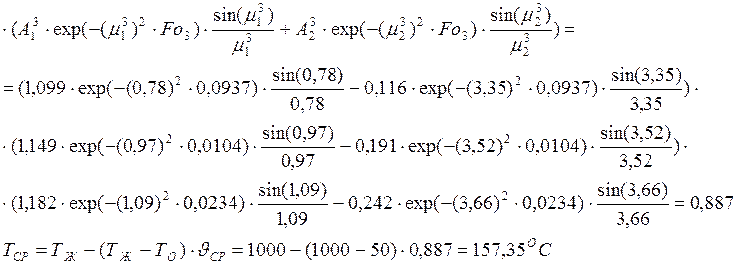
Найдем количество тепла, принятое параллелепипедом в процессе нагрева:
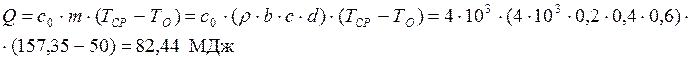
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.