Подобие физических процессов. Общие условия подобия. Следствия из условий подобия. Методы анализа размерностей. Моделирование процессов конвективного теплообмена

Таким образом, запись размерных условий однозначности в общем (буквенном) виде должна быть идентична, при этом конкретные значения, например, скорости набегающего потока или температуры стенки могут иметь различные численные величины. Если рассматривать безразмерные граничные условия, то не только их форма, но и численные значения входящих в них величин будут одинаковыми.

Из первого и второго условий подобия следует, что подобные процессы должны описываться одинаковыми (тождественными) дифференциальными уравнениями и безразмерными условиями однозначности.

В безразмерной форме математическая формулировка рассматриваемых подобных процессов одна и та же. Следовательно, рассматриваемые подобные процессы описываются единой формулой, например,  или  и т.д. Функция f₁ будет одинаковой для всех подобных процессов. То же самое можно сказать и о функции f₂ и т.д. Если система размерных уравнений достаточно сложна, то при нахождении функций f₁ и f₂ могут встретиться значительные математические трудности. Однако всегда можно утверждать, что эти функции существуют (конечно, если задача сформулирована точно).

Тогда, при соблюдении двух первых условий подобия, исследуемые процессы будут зависеть от одних и тех же критериев и только этих, первых двух условий, будет недостаточно для установления физического подобия. Нужно добавить условие, что одноименные определяющие (являющиеся аргументами функций) критерии подобных процессов должны иметь одинаковую численную величину.

В качестве примера рассмотрим решение уравнения теплопроводности в однородной однослойной плоской стенке с постоянным коэффициентом теплопроводности. Записанное в безразмерном виде () оно одинаково для любых процессов теплопроводности, следовательно, это один и тот же процесс, при этом числовые значения температур стенки, ее толщины и коэффициента теплопроводности могут быть различными.

Аналогично, при рассмотрении процессов нестационарной теплопроводности, одно и то же значение безразмерной избыточной температуры 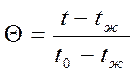 соответствует множеству различных по своим числовым значениям температур тела и жидкости. Только в частном случае может иметь место тождество процессов.

Три условия подобия составляют содержание теоремы Кирпичева – Гухмана (1931 г.).

Кроме выполнения трех условий подобия физических процессов, локальные (точечные) значения искомых переменных необходимо рассматривать в точках, характеризующихся равенством одноименных безразмерных координат, а для нестационарных процессов – и безразмерных времен. Таким образом, по существу, критериями подобия являются только определяющие критерии, прежде всего, составленные их постоянных величин.

Теорию подобия следует рассматривать как учение о характерных для каждого данного процесса обобщенных безразмерных переменных. Замена обычных размерных переменных обобщенными является основной чертой