Определение количества теплоты. Тела конечных размеров. Определение количества теплоты, отданного (полученного) телами в процессе охлаждения (нагревания). Корни характеристических уравнений. Тела конечных размеров

Лекция 10. Определение количества теплоты. Тела конечных размеров

Содержание лекции: Определение количества теплоты, отданного (полученного) телами в процессе охлаждения (нагревания). Корни характеристических уравнений. Тела конечных размеров.

Определение количества теплоты отданного (полученного) телами в процессе охлаждения (нагревания)

Рассмотрим методику определения количества теплоты отданного (полученного) телами на примере пластины. Количество теплоты, которое отдает или воспринимает пластина с обеих сторон за время от  до , должно равняться изменению внутренней энергии или энтальпии пластины за период полного охлаждения (нагревания) до температуры окружающей среды (состояние теплового равновесия):

.                              (10.1)

Тогда за любой промежуток времени от  до , или, что то же от  до  энтальпия пластины изменится на величину:

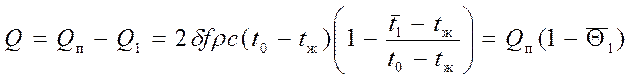,    (10.2)

где  – средняя безразмерная температура по сечению пластины в момент времени t₁.

Из соотношений (10.1) и (10.2) следует, что расчет количества теплоты, отданного или воспринятого пластиной, сводится к нахождению средней безразмерной температуры в интересующий нас момент времени. Средняя безразмерная температура для слоя пластины от оси симметрии до плоскости Х найдется в соответствии с теоремой о среднем как .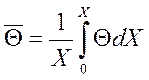

Если в это уравнение подставить под знак интеграла значение безразмерной избыточной температуры (8.11) и проинтегрировать в пределах от нуля до единицы, то получим:

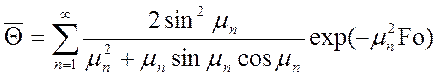.                (10.3)

Подставив в уравнение (10.2) вычисленное по формуле (10.3) значение средней температуры пластины, получим количество тепла, отданное пластиной в окружающую среду за рассматриваемый промежуток времени.

При  уравнение (10.3) принимает вид:

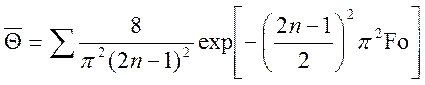.                  (10.4)

При  уравнение (10.3) принимает вид:

.                                      (10.5)

При значениях критерия Фурье  для пластины можно ограничиться первым членом ряда (10.3), тогда:

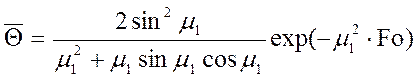.                    (10.6)

Множитель 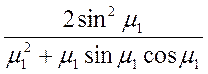 зависит только от критерия Bi и может быть представлен как некоторая функция M(Bi), и уравнение (10.6) запишется . Функция M(Bi) может быть заранее рассчитана и представлена в таблицах, тогда расчет средней температуры будет сводиться только к вычислению экспоненты.

Для определения количества теплоты, которое отдает или воспринимает цилиндр за конечное время t₁, как и для пластины, необходимо определить количество теплоты, отдаваемое (получаемое) цилиндром за время полного охлаждения (нагревания) Q_п, а также среднюю безразмерную избыточную температуру  по уравнению (11.12).

,

где                                   .                              (10.7)

Средняя безразмерная избыточная температура цилиндра может быть найдена как среднее из уравнения:

.

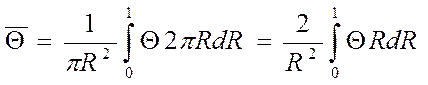После подстановки безразмерной избыточной температуры из уравнения (9.9) получаем:

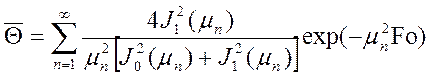,                 (10.8)

или, учитывая, что       

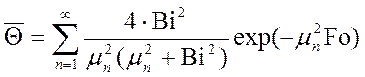.                                           (10.9)

При расчете средней температуры цилиндра в случае Fo > 0,25 также можно ограничиться одним первым членом ряда:

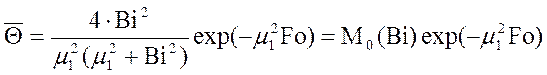.        (10.10)

Функция M₀(Bi) может быть заранее рассчитана и затабулирована.

По аналогии с пластиной и цилиндром количество теплоты, воспринимаемой шаром за конечное время t₁, определяем из уравнения

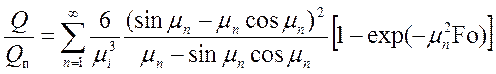,                (10.11)

где  – полное количество теплоты, которое отдает шар за время при охлаждении до температуры среды.

Корни характеристических уравнений

Расчет собственных чисел характеристических уравнений для неограниченной пластины (8.6), бесконечного цилиндра (9.10) и шара (9.23) может быть выполнен по следующим приближенным зависимостям.

Неограниченная пластина. Для определения первого собственного числа можно использовать формулу:

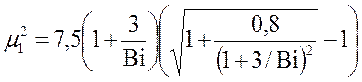.                        (10.12)

Для широкого диапазона чисел Био можно принять

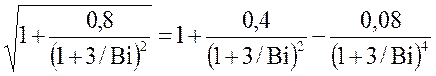, тогда

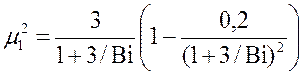.                            (10.13)

При  и  расчет корней характеристического уравнения выполняется по выражению:

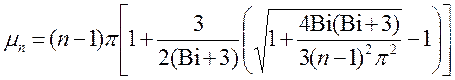,             (10.14)

если , то вычисления можно проводить по формуле:

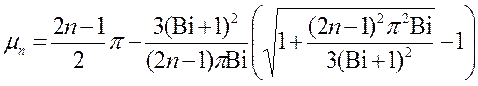.           (10.15)

Бесконечный цилиндр. Расчет первого собственного числа можно проводить по формулам:

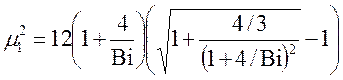                       (10.16)

или

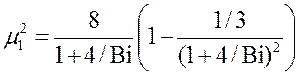.                             (10.17)

Шар. Первое собственное число при  можно определить по формуле:

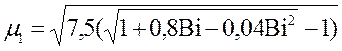.                      (10.18)

Для значений  используем выражение

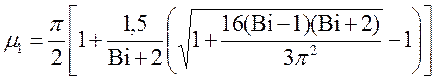.                (10.19)

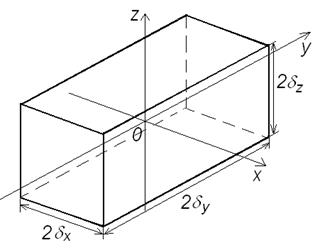Тела конечных размеров

Тела конечных размеров – параллелепипеды, прямоугольные стержни и цилиндры – можно рассматривать как тела, образованные пересечением взаимно перпендикулярных а) трех неограниченных пластин, б) двух неограниченных пластин, в) бесконечного цилиндра и неограниченной пластины,. Решение таких задач есть произведение безразмерных температур для тел неограниченных размеров, в результате пересечения которых образовалось рассматриваемое тело.                       Рис. 10.1

Рассмотрим методику определения температуры тел конечных