Дифференциальные уравнения конвективного теплообмена. Система дифференциальных уравнений конвективного теплообмена. Пример системы уравнений конвективного теплообмена

Лекция 13. Дифференциальные уравнения конвективного теплообмена

Содержание лекции: Система дифференциальных уравнений конвективного теплообмена. Пример системы уравнений конвективного теплообмена.

Система дифференциальных уравнений конвективного теплообмена

Уравнение теплоотдачи. Так как у поверхности твердого тела имеется тонкий слой неподвижной жидкости, то для этого слоя можно использовать закон Фурье: 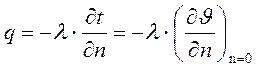. От стенки к жидкости тепло передается в процессе теплоотдачи и справедлив закон Ньютона-Рихмана: . В стационарном случае эти тепловые потоки равны, отсюда выражаем коэффициент теплоотдачи:

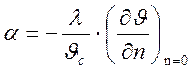.                                               (13.1)

Уравнение (13.1) называется уравнением теплоотдачи. Для его решения необходимо знать распределение температуры.

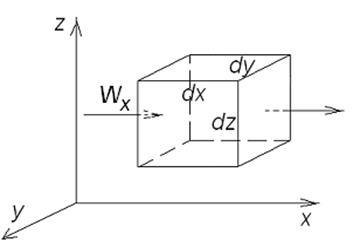
Уравнение энергии. Рассмотрим элементарный объем  (рис. 13.1). Вывод уравнения энергии аналогичен выводу уравнения теплопроводности (2.6) в случае отсутствия внутренних источников тепла. Отличия заключаются в том, что здесь вместо частной производной по времени в левой части уравнения стоит субстанциональная производная:                                                          Рис. 13.1

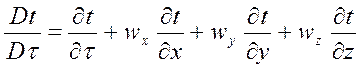, в которой первое слагаемое отвечает за локальное изменение температуры во времени в какой-либо точке, а три остальных соответствуют изменению температуры при переходе от одной точки к другой.

Тогда уравнение энергии можно записать как:

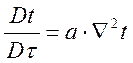.                                               (13.2)

Для решения уравнения энергии необходимо распределение скорости.

Уравнение движения основано на втором законе Ньютона: сумма сил элементарного жидкого объема равна произведению его массы на ускорение. Рассмотрим одномерное движение вдоль оси х (см. рис. 13.1); тогда для силы инерции, приходящейся на единицу объема, запишем: 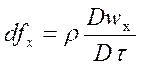. Так как на объем действуют три вида сил: объемные (массовые) , поверхностные 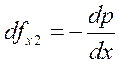 и вязкие 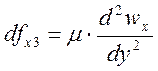, то уравнение одномерного движения вдоль оси х будет иметь вид:

.

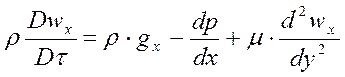Если движение происходит во всех направлениях, то описание усложняется. В общем случае трехмерного движения несжимаемой жидкости поле скоростей описывается тремя уравнениями движения, каждое соответственно в проекциях сил на оси x, y и z:

,

,

.

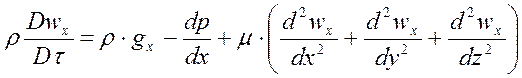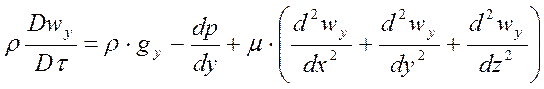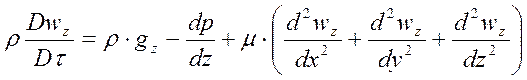Эти уравнения называют уравнениями Навье-Стокса, все они имеют размерность силы, отнесенной к единице объема.

В общем случае скорость изменяется по координатам и во времени, а субстанциональные производные для скоростей будут иметь вид:

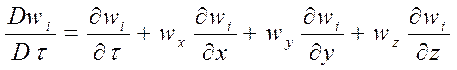, здесь i = x, y, z, а первые слагаемые субстанциональных производных характеризуют изменение скорости во времени в какой-либо точке жидкости, т.е. локальное изменение скорости; остальные три слагаемых в правых частях – изменение скорости при переходе от точки к точке.

Используя векторную форму записи, получаем уравнение:

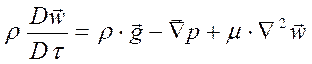, в котором не учитывается зависимость физических параметров от температуры, в частности плотности, хотя свободное движение жидкости как раз и характеризуется разностью плотностей. Чтобы уравнения движения описывали свободное движение, нужно учесть изменение плотности.

Так как в настоящее время нет универсального уравнения вида , то будем использовать приближение температурного коэффициента объемного расширения, который будем считать постоянной величиной (это условие сравнительно хорошо выполняется для газов и хуже для капельных жидкостей) 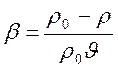, где  – температурный напор, r соответствует температуре t, r₀ – температуре t₀; тогда , подставим это выражение в векторное уравнение движения:

.

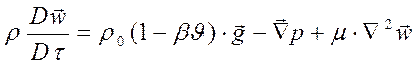Рассмотрим первое слагаемое в правой части полученного уравнения , которое есть алгебраическая сумма силы тяжести r₀g и подъемной силы r₀gbu. Для многих задач можно ограничиться только учетом подъемных сил rgbu (здесь r – фиксированное значение плотности). Если при этом считать плотность постоянной, получаем уравнение движения для несжимаемой жидкости:

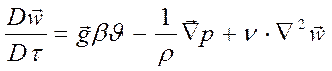                                   (13.3)

Так как в уравнение движения (13.3) входит еще одна неизвестная величина – плотность, то система уравнений по-прежнему не является замкнутой. Необходимо добавить еще одно уравнение, характеризующее изменение массы жидкости.

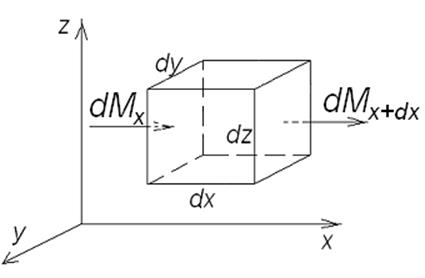Уравнение неразрывности (сплошности). Выделим в потоке движущейся жидкости неподвижный элементарный объем dv и посчитаем массу протекающей через него жидкости (рис. 13.2).

В направлении оси x в параллелепипед втекает масса жидкости: