%Вычислим критеририй хи-квадрат
Xi2=0;
for i=1:nTime-1
Xi2 = Xi2 + ((Emp_function(i) - q_Teor(i))^2) /(q_Teor(i))
end
k = nTime - 1; %Количество интервалов
m = 1; %Количество параметров, которые оценивались
r = k-m-1; %Число степеней свободы
Xi2_Tab_1 = chi2inv(1-alfa1, r) %Табличное значение критерия хи-квадрат с уровнем значимости alfa1
Xi2_Tab_2 = chi2inv(1-alfa2, r)%Табличное значение критерия хи-квадрат с уровнем значимости alfa2
disp(sprintf('Значение критеририя Пирсона: %f', Xi2));
disp(sprintf('При уровне значимости %.2f критерий Пирсона: %f',alfa1,Xi2_Tab_1));
disp(sprintf('При уровне значимости %.2f критерий Пирсона: %f',alfa2,Xi2_Tab_2));
%Вычислим критерий Колмагорова-Смирнова
dn = max(abs(Emp_function - q));
kvantil_1 = sqrt(-(log(alfa1/2)/2));
kvantil_2 = sqrt(-(log(alfa2/2)/2));
stat = sqrt(N) * dn;
disp(sprintf('Значение критеририя Колмогорова-Смирнова: %f', dn));
disp(sprintf('Квантиль распределения, соответствующая уровню значимости %.2f:%f',alfa1,kvantil_1));
disp(sprintf('Квантиль распределения, соответствующая уровню значимости %.2f:%f',alfa2,kvantil_2));
Оценка среднего времени безотказной работы
Вычисляется по формуле:
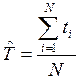
где ![]() – совокупность значений наработки устройств
– совокупность значений наработки устройств
![]() ,
,
N – общее количество устройств.
Оценка среднего времени безотказной работы: 0.418553
Оценка выборочной дисперсии времени безотказной работы
Вычисляется по формуле:
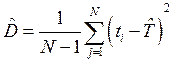
Оценка выборочной дисперсии времени безотказной работы: 163.353555
Оценка интенсивности отказов как функция времени работы
Вычисляется по формуле:
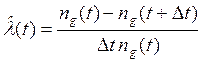
где ![]() - число устройств, исправно работавших в момент
- число устройств, исправно работавших в момент ![]() ,
,
![]() - малый интервал времени.
- малый интервал времени.
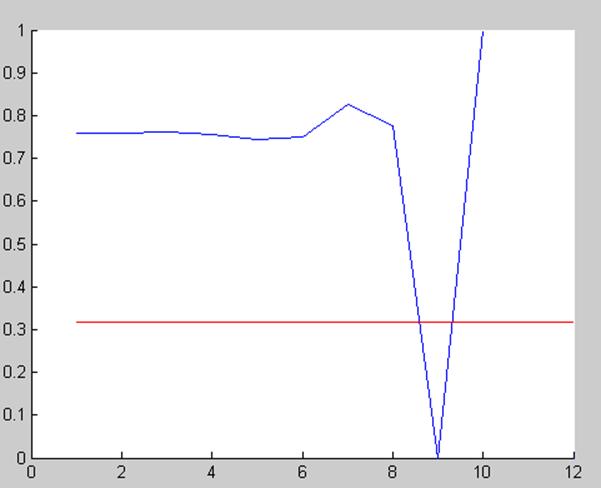
Рис.1. Интенсивность отказов как функция времени работы
Гистограмма распределения отказов
Гистограмма распределения отказов
показывает, сколько устройств отказало в течение малого интервала времени от t до t + ![]() .
.
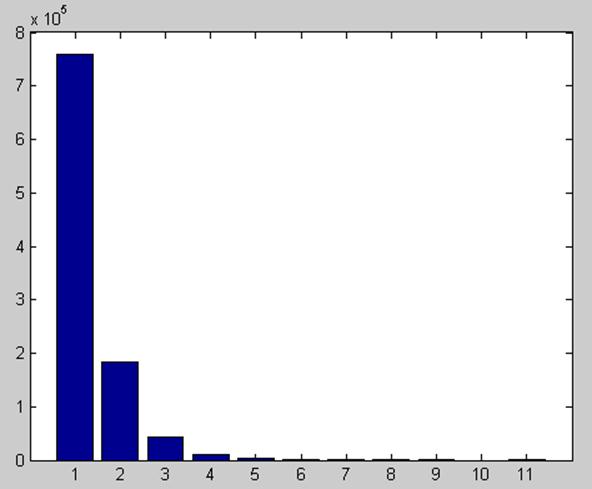
Рис.2. Гистограмма
распределения количества отказов в интервалах от t до t +![]()
Гипотеза о законе распределения случайной величины
Исходя из графиков функции распределения и плотности распределения выдвигается гипотеза о том, что случайная величина имеет экспоненциальное распределение.
Проверка гипотезы критерием Пирсона
Область значений с.в. разбивается
на непересекающиеся классы ![]() .
Пусть
.
Пусть ![]() обозначает число значений выборки,
содержащееся в классе
обозначает число значений выборки,
содержащееся в классе ![]() . Разбиение на классы
должно быть таким, чтобы при всех
. Разбиение на классы
должно быть таким, чтобы при всех ![]() выполнялось
условие
выполнялось
условие ![]() . Обозначим через
. Обозначим через ![]() вероятность класса
вероятность класса ![]() , вычисленную по теоретическому
распределению.
, вычисленную по теоретическому
распределению.
Тогда значение критерия Пирсона вычисляется по формуле:
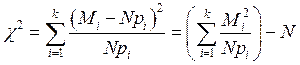
Плотность
![]() -распределения с
-распределения с ![]() степенями свободы имеет вид
степенями свободы имеет вид
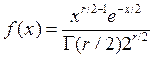 .
.
Распределение
![]() табулировано, и его таблицы
можно найти во многих справочных пособиях. Однако в настоящее время
целесообразнее воспользоваться компьютером для подсчета необходимых значений
функции распределения. В частности, если доступна статистическая библиотека
пакета MATLAB, то можно воспользоваться функцией chi2inv(1-
табулировано, и его таблицы
можно найти во многих справочных пособиях. Однако в настоящее время
целесообразнее воспользоваться компьютером для подсчета необходимых значений
функции распределения. В частности, если доступна статистическая библиотека
пакета MATLAB, то можно воспользоваться функцией chi2inv(1-![]() , r), в которую передаются уровень значимости в виде входного
параметра 1-
, r), в которую передаются уровень значимости в виде входного
параметра 1-![]() и
число степеней свободы в виде второго параметра r . Функция возвращает
пороговое значение
и
число степеней свободы в виде второго параметра r . Функция возвращает
пороговое значение ![]() такое, что
такое, что
![]() ,
,
где ![]() –
кумулятивная функция
–
кумулятивная функция ![]() -распределения.
-распределения.
Число степеней свободы вычисляется по формуле:
![]() =
=![]()
где k – количество классов,
m – количество параметров распределения.
Если ![]() <
< ![]() , то гипотеза при уровне значимости
, то гипотеза при уровне значимости ![]() принимается (иначе отвергается).
принимается (иначе отвергается).
Значение критеририя Пирсона: 0.004393
При уровне значимости 0.10 критерий Пирсона: 14.683657
При уровне значимости 0.01 критерий Пирсона: 21.665994
Гипотеза принимается при уровне значимости 0.10.
Гипотеза принимается при уровне значимости 0.01.
Проверка гипотезы критерием Колмогорова-Смирнова
Критерий вычисляется по формуле:
![]() .
.
где ![]() -
эмпирическая функция распределения,
-
эмпирическая функция распределения,
![]() - теоретическая
функция распределения.
- теоретическая
функция распределения.
Квантиль распределения,
соответствующий уровню значимости ![]() , вычисляется по
формуле:
, вычисляется по
формуле:
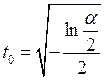
Если ![]() < t0 , то гипотеза
при уровне значимости
< t0 , то гипотеза
при уровне значимости ![]() принимается (иначе
отвергается).
принимается (иначе
отвергается).
Значение критерия Колмогорова-Смирнова (![]() ):0.758721
):0.758721
Квантиль распределения, соответствующая уровню значимости 0.10:1.223873
Квантиль распределения, соответствующая уровню значимости 0.01:1.627624
Гипотеза принимается при уровне значимости 0.10.
Гипотеза принимается при уровне значимости 0.01.
Графики эмпирической и гипотетической функции распределения
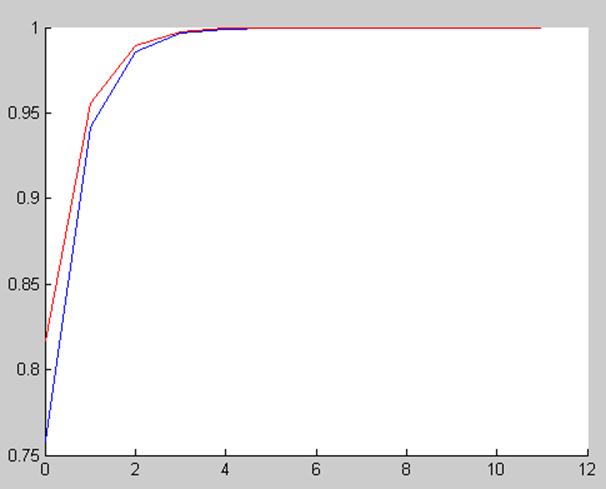
Рис.3. Эмпирическая и гипотетическая функция распределения F(t)
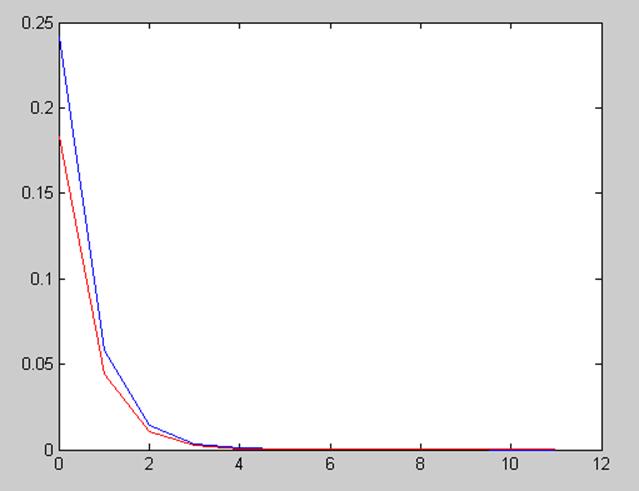
Рис.5. Вероятность безотказной работы P(t) в течение времени t
Вывод
В ходе лабораторной работы по экспериментальным данным были оценены основные показатели надежности устройства. Была построена модель распределения вероятностей наработки на отказ. Была выдвинута гипотеза о том, что случайная величина, описывающая отказы устройства, подчиняется геометрическому закону распределения. Эта гипотеза была проверена с помощью критерия Пирсона и критерия Колмогорова-Смирнова и принята с уровнями значимости 0.1 и 0.01.
Из графиков видно, что в раннем периоде жизни устройства наблюдается сравнительно большое число отказов, вызванных, видимо, начальными недостатками или дефектами. Этот период называется периодом ранних отказов или периодом приработки. Далее с течением времени количество отказов уменьшается геометрически.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.