Определение давления и проверка прочности грунта на подошве жесткого ленточного фундамента

ДОМАШНЕЕ ЗАДАНИЕ № 2

Определение давления и проверка прочности грунта на подошве жесткого ленточного фундамента

Задание.

  I.  По исходным данным своего варианта (табл. 1.1) рассчитать коэффициент пористости грунта ε, степень влажности I_w и показатель консистенции I_L (для глинистых грунтов).

  II.  Пользуясь рассчитанными характеристиками, по таблице СНиП       2.02.01-83^* (табл. 1-9 приложения) определить вид грунта, его состояние и нормативные прочностные и деформационные характеристики: сцепление c_n, угол внутреннего трения φ_n, модуль общей деформации Е_o и условное расчетное давление R_o.

III.  По заданной нагрузке и условному расчетному давлению, пренебрегая эксцентриситетом силы, рассчитать ширину подошвы фундамента. С учетом эксцентриситета нагрузки рассчитать распределение давления по подошве жесткого фундамента, проверить прочность грунта под наиболее нагруженным краем подошвы по начальному критическому давлению и оценить глубину развития области предельного напряженного состояния.

Последовательность выполнения:

1.  Рассчитываются коэффициент пористости в условиях природного сложения и влажности по формуле

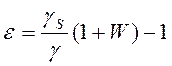                                   (1.1)

и степень влажности грунта:

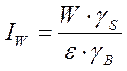,                                         (1.2)

где  γ_S – удельный вес частиц грунта, кН/м³;

γ – удельный вес природного грунта, кН/м³;

W – естественная влажность;

γ_B – удельный вес воды, принимаемый 10 кН/м³.

Для глинистых грунтов рассчитывается число пластичности по формуле

                                        (1.3)

и показатель консистенции:

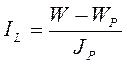,                                          (1.4)

где  W_L – влажность на границе текучести;

W_P – влажность на границе раскатывания. 

2.  Для песчаных грунтов определяется наименование по степени влажности и плотность сложения из табл. 1 и 2 приложения.

Для глинистых грунтов (супеси, суглинки и глины) определяется наименование и состояние грунта по консистенции в соответствии с табл. 3 и 4 Приложения.

3.  Определяются нормативные значения сцепления c_n и угла внутреннего трения φ_n, модуль общей деформации Е_o и условного расчетного давления R_o из табл. 5 – 9 приложения. Вычисляются расчетные значения сцепления с = с_n / γ_g(c) и угла внутреннего трения φ = φ_n / γ_g(φ). Коэффициент надежности γ_g принимается по табл. 15 приложения.

4.  Рассчитывается предварительное значение ширины подошвы ленточного фундамента по условному расчетному давлению без учета эксцентриситета нагрузки, м:

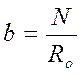,                                                  (1.5)

где  N – нагрузка на 1 м длины фундамента, кН/м;

R_o – условное расчетное давление, кПа.

В этих расчетах собственный вес фундамента входит в нагрузку N.

Полученное значение b округляется в большую сторону до 100 мм.

5.  Определяется давление в краевых точках А и В подошвы фундамента по формуле сопротивления материалов с эксцентриситетом нагрузки и строится график распределения давления (линия 1 на рис. 1.1), кН/м²:

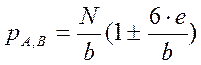,                                        (1.6)

где  b – уточненное значение ширины подошвы, м;

e – эксцентриситет нагрузки, м;

знак «+» соответствует давлению в точке В, а знак «-» – в точке А для данного направления эксцентриситета.

6.  Определяется начальное критическое давление в краевой точке В по формуле

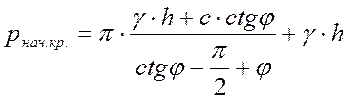,                        (1.7)

где  γ – удельный вес природного грунта, кН/м³;

с – расчетное сцепление грунта, кН/м²;

φ – расчетный угол внутреннего трения грунта, радиан;

h – глубина заложения подошвы, м.

7.  Давление в точке В от внешней нагрузки (максимальное значение давление по подошве) сравнивается с начальным критическим давлением:

                                                    (1.8)

Если условие (1.8) выполняется, области предельного напряженного состояния не образуются, ширину подошвы фундамента принять как в п. 4, и переходить к выполнению п. 10. В случае, если по условию (1.8) получается излишний запас, необходимо уменьшить ширину подошвы фундамента в пределах этого условия с округлением в 0,1 м.

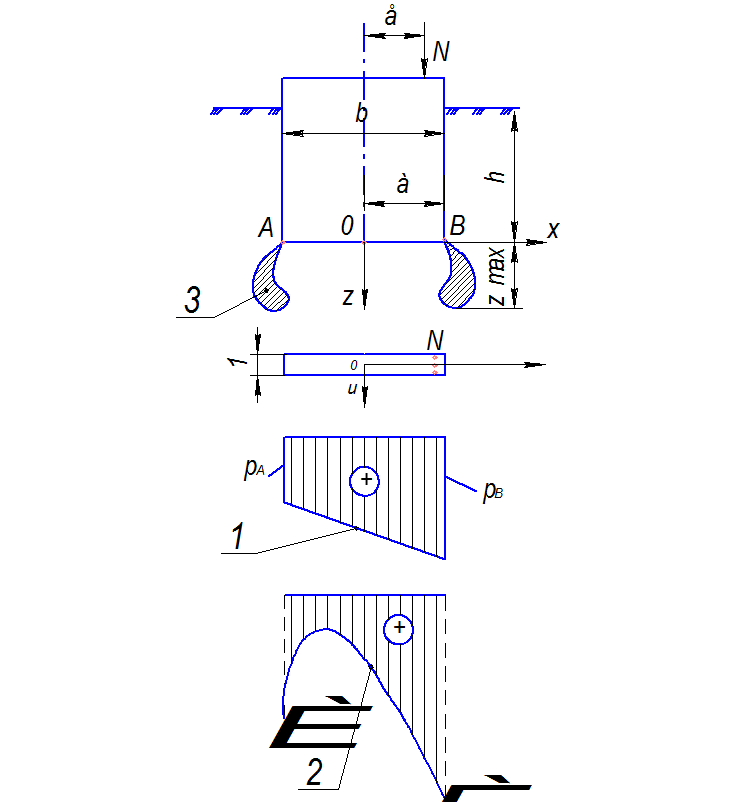
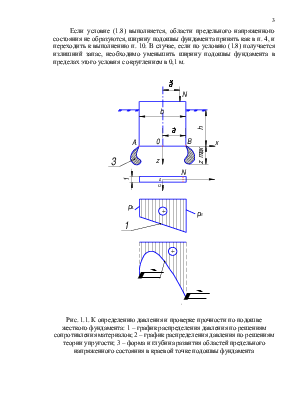
Рис. 1.1. К определению давления и проверке прочности по подошве жесткого фундамента: 1 – график распределения давления по решениям сопротивления материалов; 2 – график распределения давления по решениям теории упругости; 3 – форма и глубина развития областей предельного напряженного состояния в краевой точке подошвы фундамента

8.  Если р_В > р_нач.кр., то образуется область предельного напряженного состояния. Максимальная глубина развития области предельного напряженного состояния в краевой точке В определяется по формуле

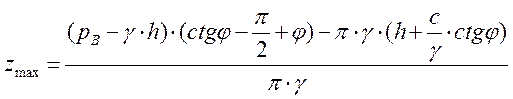,                (1.9)

где  р_В – давление в точке В, рассчитанное по формуле (1.6), кН/м².

9.  Глубина развития области предельного напряженного состояния не должна превышать заданной допустимой величины, м:

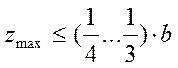,                               (1.10)

Если условие (1.10) соблюдается, то прочность грунта по подошве считается достаточной. В противном случае необходимо увеличить ширину подошвы фундамента до выполнения условия (1.10).

10.Рассчитывается распределение давления по подошве жесткого ленточного фундамента по формуле теории упругости:

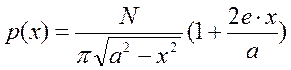,                      (1.11)

где 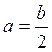  – половина ширины подошвы фундамента, м;

х – текущая горизонтальная координата точки подошвы, в которой определяется давление; х задавать значения: -0,75·а; -0,5·а; 0; +0,5·а; 0,75·а; 0,9·а.

По результатам расчета строится график распределения давления по решениям теории упругости. Для случая, когда эксцентриситет нагрузки        е < а/2, график имеет вид кривой 2 на рис. 1.1. По формуле теории упругости значение давления в краевых точках стремится к ∞ и не имеет конечного значения. Поэтому для оценки несущей способности грунта по подошве в краевых точках, где зарождаются области предельного напряженного состояния, берутся давления, определенные по решениям сопротивления материалов.