




Лекция 10
ИЗМЕНЕНИЕ ОСАДОК ВО ВРЕМЕНИ
Дифференциальное уравнение теории фильтрационной консолидации
Осадки
грунтов не заканчиваются сразу по окончании строительства. Как правило, полная
осадка 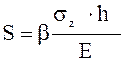 , где β=0,8- коэффициент, характеризующий
деформативность грунтов под нагрузкой, для различных грунтов достигается в
разное время. Водонасыщенные пластичные и особенно текучепластичные (слабые)
грунты дают наибольшие осадки, весьма медленно затухающие и создают для
строителей наибольшие затруднения. Осадки сооружений на таких грунтах могут
достигать сотен см и протекать десятки и сотни лет. При неравномерных осадках
оснований и больших скоростях осадок могут иметь место хрупкие (аварийные)
разрушения конструкций, при малых скоростях осадок – медленные деформации
ползучести.
, где β=0,8- коэффициент, характеризующий
деформативность грунтов под нагрузкой, для различных грунтов достигается в
разное время. Водонасыщенные пластичные и особенно текучепластичные (слабые)
грунты дают наибольшие осадки, весьма медленно затухающие и создают для
строителей наибольшие затруднения. Осадки сооружений на таких грунтах могут
достигать сотен см и протекать десятки и сотни лет. При неравномерных осадках
оснований и больших скоростях осадок могут иметь место хрупкие (аварийные)
разрушения конструкций, при малых скоростях осадок – медленные деформации
ползучести.
В настоящее время для водонасыщенных (слабых) грунтов наиболее широко применяется теория фильтрационной консолидации грунтов.
Предпосылки использования теории фильтрационной консолидации:
1) грунт полностью водонасыщен, вода и скелет грунта объемно несжимаемы, вода гидравлически непрерывна;
2) скелет грунта принимается линейно деформируемым: напряжения в котором мгновенно вызывают его деформации;
3) Грунт не обладает структурной прочностью, внешнее давление, прикладываемое к нему, в первый момент времени полностью передается на воду;
4) фильтрация воды в порах грунта полностью подчиняется закону Дарси; изменение пористости определяется законом уплотнения.
Дифференциальное уравнение одномерной задачи теории фильтрационной консолидации
Описывает протекание во времени осадок полностью водонасыщенного грунта при уплотнении его равномерно распределенной нагрузкой в условиях односторонней фильтрации воды.
Примем, что в начальный момент времени грунтовая масса находится в статическом состоянии, поровое давление воды при этом равно нулю, т.е.
t = 0, p = pпор= рw; рэфф = рz=0.
Для слоя грунта, лежащего на водоупоре граничные условия следующие:
При z=0 и t>0 имеем pэфф= р, рw= 0. Незначительная некорректность просматривается в начальном моменте времени. Граничное условие будем рассматривать при t > 0.
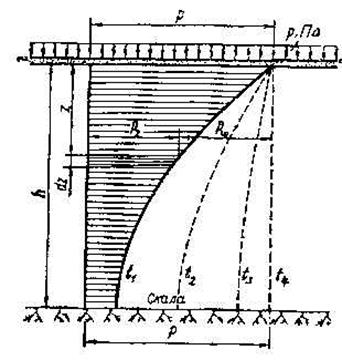
Рис. 1. Схема распределения давлений в скелете грунта (рz) и в поровой воде (рw) в водонасыщенном слое при сплошной нагрузке для разных промежутков времени
Очевидно, что
рz + рw = р, (1)
т.е. на любой глубине z от дренирующей поверхности давление в поровой воде и давление в скелете грунта равно внешнему давлению р.
Для элементарного слоя dz на глубине z в грунтовой массе увеличение расхода воды q равно уменьшению пористости грунта n, т.е.
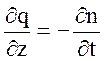 (2)
(2)
Преобразуем левую и правую части уравнений:
Для
левой части по закону Дарси 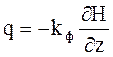 (3)
(3)
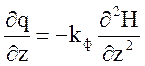 (4)
(4)
Принимая, что напор в воде Н равен давлению в воде рw, деленному на удельный вес γw, из выражения (1) следует:
рw = р – рz; Н = рw/
γw или Н = (р - рz) / γw
, откуда
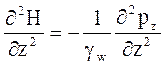 (5)
(5)
учитывая выражение (4), получим
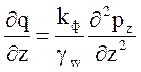 (6)
(6)
Учитывая, что пористость грунта n = e/(1+ e), пренебрегая в знаменателе изменением коэффициента пористости е по сравнению с единицей
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.