Задачи, решаемые по топографическому плану и карте. Определение расстояний на топографической карте с помощью линейного и поперечного масштабов. Определение крутизны ската. Определение планового положения точек. Определение координат и углов на планах и картах

расстояние между крестиками (концами ножек циркуля-измерителя) будет

Поперечный масштаб при всех его достоинствах не может обеспечить точность выше определенного предела, зависящего от свойств человеческого глаза. Глаз человека в состоянии совмещать острие ножки циркуля с точкой на плане, точку с точкой, штрих со штрихом с точностью около 0,1 мм *, если они находятся на расстоянии 25 см от глаза. Из этого следует, что детали объектов местности (выступы, изгибы), выражающиеся на плане линиями менее 0,1 мм, изобразить нельзя. Поэтому при изображении деталей объектов местности на плане руководствуются точностью масштаба, которая представляет длину горизонтального приложения линии на местности, соответствующую 0,1 мм на плане. Например, точность масштаба 1 : 10 000 равна 1 м, масштаба 1 : 5000 — 0,5 м и др. Для определения точности масштаба следует знаменатель численного масштаба М разделить на 10000. Для карты масштаба 1:25000 точность  равна 2,5 м.

Определение крутизны ската

Крутизна ската характеризуется углом наклона v, который образует линия местности, например АВ, с горизонтальной плоскостью Р (рис. 22).

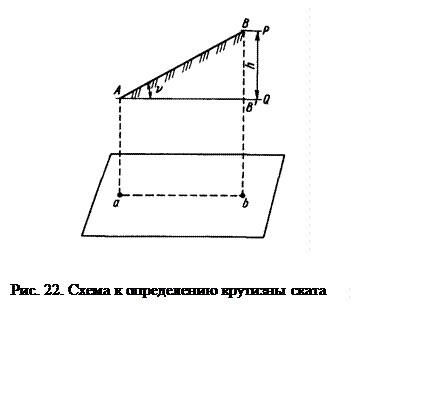Из прямоугольного треугольника АВВ^’ следует: 

tgν= h/s,                                                         (3.1)

где h — высота сечения рельефа, s — заложение.

Зная тангенс, находят значение угла наклона.

Крутизну ската характеризуют также уклоном i:

                                                   i = tgν                                                               (3.2)

Уклон линии выражается в процентах или промилле , т. е. тысячных долях  единицы.

Пример. Определить угол наклона и уклон ската местности между горизонталями на плане масштаба 1:1000, если заложение равно 20мм, высота сечения рельефа h =1,0 м.

На местности заложению будет соответствовать длина отрезка, равная ab=20 мм х 1000= 20000 мм =20 м. По формулам (3.1) и (3.2) tgν=1/20=0,05, откуда   i = 5% , а ν = 2,9^о.

Как правило, при работе с картой или планом угол наклона либо уклон ската определяют, пользуясь графиками (рис. 24, а, б), называемыми масштабами (или шкалами) заложений.

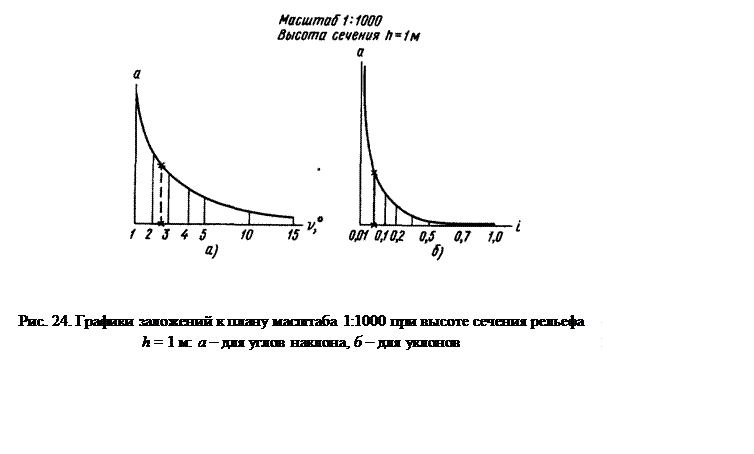Для этого с плана раствором циркуля берут заложение между двумя горизонталями по данному скату, затем по графику находят то место, где расстояние между кривой и горизонтальной прямой равно этому заложению. Для найденной таким образом ординаты прочитывают значение ν или iпо горизонтальной прямой (на приведенных графиках отмечено звездочками:        ν =2,9°, i =0,05=5%).

Определение планового положения точек

Определение координат и углов на планах и картах

Наличие плана (карты) позволяет получить большое количество информации о местности и использовать ее для решения различных инженерных задач.

Северная и южная линии внутренней рамки листа карты (рис. 25, а) являются параллелями, а западная и восточная — меридианами. На листе карты имеются географические координаты углов рамки. Каждая сторона ее разбита на целые минуты по долготе и широте, что представляет собой минутную рамку. Для удобства пользования отрезки этой рамки через один залиты черным цветом. Отрезки abи beсоответствуют одной минуте долготы, а отрезки deи ef— одной минуте широты.

Кроме этого, на карте (плане) имеется сетка прямоугольных координат. На рис. 25 приведена километровая сетка, т. е. расстояние между линиями по осям Xи Yравно 1 км. На краях карты прямоугольная сетка оцифрована с внутренней стороны рамки. Наличие на карте системы прямоугольных координат позволяет получить значения координат любой точки на карте (плане). Пусть имеется на карте точка С. Ближайшая юго-западная точка пересечения координатной сетки имеет координаты    Х = 6065 км, Y= 4311 км.

Опустив перпендикуляры из точки С на ближайшие координатные линии, получим приращения координат ΔХ _с и  ΔY _с .

Тогда прямоугольные координаты точки С:

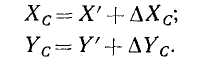
Для получения значенийи измеряют циркулем-измерителем эти отрезки и, пользуясь поперечным или линейным масштабом, определяют их значения в метрах. В примере  . Тогда искомые координаты точки С будут

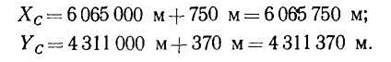
Таким образом, точка С удалена на расстояние 6 065 750 м от плоскости экватора и находится в четвертой зоне на расстоянии 311370 м от начала системы координат этой зоны, или с учетом сдвига начала