Частица в бесконечной прямоугольной потенциальной яме

Лекция № 9.

Частица в бесконечной прямоугольной потенциальной яме.

Ключевые слова:

стандартные требования к волновой функции граничные условия энергетический спектр и волновые функции частицы в яме графики волновой функции и плотности вероятности

                                     

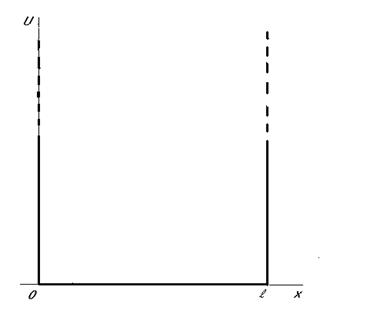
Рис.5. Бесконечная прямоугольная потенциальная яма.

Частица заключена между двумя абсолютно непроницаемыми стенками (рис5). Нахождение частицы за пределами указанной области означало бы наличие у неё бесконечной энергии, что недопустимо. Таким образом, при x<0  и при x>0,  Ψ(x

)≡0.

В области 0 ≤ x ≤ l волновая функция удовлетворяет уравнению

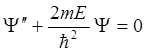      .                       (2.22)

С учетом того, что энергия частицы в заданном потенциале неотрицательна, выразим её через квадрат действительного числа k:

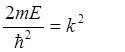 и получим решение в виде

                                            (2.23)

Волновая функция должна удовлетворять стандартным требованиям:

а) конечности б) непрерывности в) однозначности.

Функция (2.23) уже удовлетворяет требованиям а) и в), а из требования её непрерывности вытекают граничные условия, позволяющие окончательно определить волновую функцию и энергетический спектр частицы:

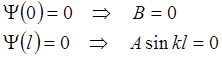                                                  (2.24)

Коэффициент А не может быть равен 0, иначе волновая функция всюду обращается в 0, что означает отсутствие частицы в яме. Поэтому

                          (2.25)

Отметим, что нумерация состояний начинается с 1, т.к. при n=0 имеем Ψ(x

)≡0 и  частица в яме отсутствует.

Выражая k из условия (2.25) и подставляя его в выражение для энергии и в волновую функцию (2.23) окончательно получим:

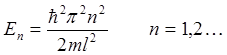                                     (2.26)

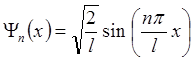                    .                       (2.27)

Коэффициент в волновой функции получен из условия нормировки:

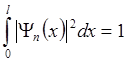.                                                        (2.28)

Обсудим полученные решения. Расстояние между соседними уровнями энергии возрастает по мере роста квантового числа n. На первый взгляд может показаться, что это противоречит принципу соответствия Бора, согласно которому по мере возрастания энергии результаты квантовомеханического расчета должны всё более приближаться к своему классическому пределу и, следовательно, дискретность энергетического спектра характерная для квантовой механики должна постепенно нивелироваться. На самом деле противоречия нет, в чём нетрудно убедиться при более внимательном рассмотрении. Дело в том, что надо оценивать не абсолютную, а относительную разницу энергий, а в этом случае из формулы (2.26) следует

в полном согласии с принципом соответствия.

Графики волновой функции и плотности вероятности при n=1,2,3 представлены на рис.6. Волновая функция основного состояния не имеет узлов и симметрична относительно центра ямы (рис.6а). У волновой функции следующего по энергии состояния появляется узел и она  антисимметрична относительно точки l/2. При увеличении квантового числа n ещё на 1 снова получаем симметричную функцию, но уже с двумя узлами. Легко убедиться, что подмеченная тенденция изменения числа узлов и четности волновой функции сохраняется и при дальнейшем росте квантового числа.

        

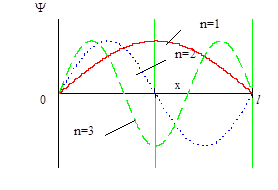
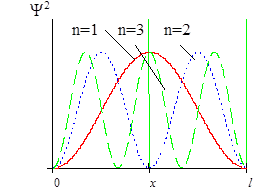
а)                                                               б)

Рис.6. Волновые функции (а) и распределение вероятности

координаты (б) частицы в потенциальной яме.

В основном состоянии частицу с наибольшей вероятностью можно обнаружить в центре ямы (рис.6б). С ростом квантового числа n число максимумов увеличивается и при больших квантовых числах распределение стремится к классическому пределу, с равной вероятностью обнаружения частицы в любом месте ямы.