Уравнение Шредингера. Вектор плотности потока вероятности. Стационарное уравнение Шредингера. Свойства стационарных состояний

Лекция №5.

План лекции:

уравнение Шредингера,

вектор плотности потока вероятности,

стационарное уравнение Шредингера,

свойства стационарных состояний.

Ключевые слова:

уравнение Шредингера

вектор плотности потока вероятности

стационарные состояния

Уравнение Шредингера.

Рассмотрим теперь вопрос о том, как состояние системы меняется со временем. Указанное изменение выражается в явной зависимости волновой функции от времени. Эта зависимость определяется основным динамическим уравнением квантовой механики, которое, как следует из принципа суперпозиции, должно быть линейным. Кроме того, из принципа причинности следует, что это уравнение не может содержать производные по времени выше первого порядка. Действительно решение дифференциального уравнения n-ого порядка содержит n постоянных интегрирования, определение которых потребовало бы задания n начальных условий. В действительности имеется только одно начальное условие, которое состоит в задании волновой функции в начальный момент времени.

С учётом высказанных выше общих соображений можно представить искомое уравнение в виде

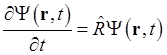                                            (1.66), где - неизвестный пока линейный оператор, а r – совокупность координат системы. Ряд соображений указывает на то, что оператор  с точностью до константы совпадает с оператором Гамильтона: 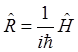. В частности,  можно показать, что при таком выборе в классическом пределе получается уравнение Гамильтона-Якоби классической механики. Итак, основное динамическое уравнение квантовой механики может быть представлено в виде

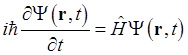                                           (1.67)

и носит название уравнения Шредингера.

Это линейное уравнение в частных производных, содержащее первую производную по времени. Последнее обстоятельство, как уже отмечалось, связано с принципом причинности квантовой механики, а его линейность вытекает из принципа суперпозиции.

Уравнение обратимо во времени. Нетрудно убедиться, что уравнение сохраняет свой вид, если наряду с заменой  осуществить замену волновой функцию  на комплексно ей сопряжённую функцию . Таким образом, операция комплексного сопряжения, проведённая над волновой функцией эквивалентна изменению направления времени.

Вектор плотности потока вероятности.

Запишем уравнение Шредингера, а также комплексно сопряжённое ему уравнение в виде

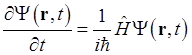                                                                                         (1.68)

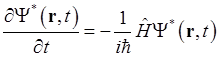                                                                                   (1.69).

Домножим первое уравнение на и сложим оба уравнения. Тогда получим

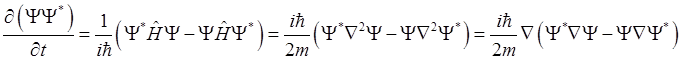
Полученное выражение представляет собой уравнение непрерывности

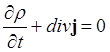                                                   (1.70)

где  - плотность вероятности, а вектор 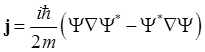называется вектором плотности потока вероятности. Модуль вектора численно равен вероятности прохождения частицы в единицу времени через единичную площадку нормальную к вектору j. Из уравнения (1.70) вытекает непрерывность волновой функции и её первой производной. В особых случаях производная может терпеть разрыв (см. семинар 2.1). Уравнение (1.70) выражает закон сохранения числа частиц в квантовой механике. Проинтегрируем уравнение (1.70) по объёму

.

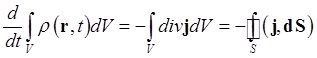Распространяя объём интегрирования на всё пространство и, полагая волновую функцию на бесконечности равной нулю, получим

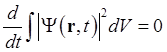                                                 , откуда вытекает закон сохранения условия нормировки волновой функции

                                          (1.71).

Стационарное уравнение Шредингера.

В постоянном внешнем поле, когда потенциальная функция и, следовательно, оператор Гамильтона не зависят явно от времени, уравнение Шредингера допускает разделение переменных. Представим волновую функцию в виде

                                            (1.72).

Подставляя функцию в уравнение Шредингера получим после деления уравнения на

.

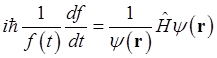Поскольку левая часть уравнения зависит только от времени, а правая только от пространственных координат, то ясно, что обе части уравнения не зависят ни от каких переменных и их можно приравнять постоянной величине, имеющей размерность энергии. Обозначая эту величину буквой Е, получим

                   (1.73)

        .                                 

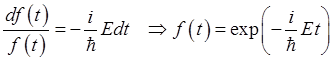Уравнение (1.73) называется стационарным уравнением Шредингера. Оно представляет собой уравнение для собственных функций и собственных значений оператора Гамильтона и описывает стационарные состояния с определённым значением энергии Е.  Для системы состоящей из одной частицы находящейся во внешнем поле , после подстановки оператора Гамильтона в явном виде стационарное уравнение Шредингера принимает вид

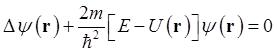                                 (1.74).

Стационарное уравнение Шредингера позволяет определить энергетический спектр системы. Этот спектр может быть как непрерывным, так и дискретным. При этом его характер может меняться в зависимости от энергии – он может быть дискретным в одной области значений энергии и непрерывным в другой. Важнейшим фактором для определения характера энергетического спектра являются стандартные требования к волновой функции. Примеры решения стационарного уравнения Шредингера для ряда важных частных случаев будут рассмотрены в главе 2.

Свойства стационарных состояний.

Стационарными называются состояния с определённой энергией системы. Это определение стационарных состояний является одновременно и одним из его свойств.

Волновые функции стационарных состояний можно представить в виде

                                            (1.75), где координатная часть волновой функции удовлетворяет стационарному уравнению Шредингера (1.73).

Плотность вероятности и плотность потока вероятности стационарных состояний не зависит от времени. Действительно

.

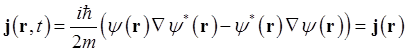Средние значения и вероятности получения собственных значений наблюдаемых, операторы которых не зависят явно от времени, являются постоянными. Для доказательства первого утверждения запишем выражение для среднего значения наблюдаемой, оператор которой не зависит явно от времени

.

Пусть - собственная функция оператора , принадлежащая собственному значению .  Найдём вероятность получения k-ого собственного значения наблюдаемой F в стационарном состоянии с волновой функцией вида (1.75). Эта вероятность определяется квадратом модуля коэффициента C_k  в разложении волновой функции (1.75) по собственным функциям оператора . Коэффициент C_k определяется выражением вида (1.24), которое модифицировано с учётом зависимости волновой функции от пространственных координат и времени

.

Как следует из предыдущей формулы , что и доказывает сделанное выше утверждение.

Волновую функцию произвольного состояния системы можно представить в виде разложения по волновым функциям стационарных состояний. Для случая дискретного энергетического спектра это разложение имеет вид

                                (1.76).