Свободная частица. Волновая функция свободной частицы. Волновой пакет. Расплывание волнового пакета

Лекция 8.

Свободная частица.

Ключевые слова:

волновая функция свободной частицы

волновой пакет

расплывание волнового пакета

Уравнение Шредингера для свободной частицы имеет вид:

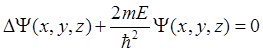  .                           (2.8)

Волновую функцию Ψ(x,y,z) можно представить в виде произведения функций от отдельных координат:

  .                             (2.9)

Подстановка функции (2.9)  в (2.8) приводит к разделению переменные в уравнении. В результате получим три одномерных уравнения вида:

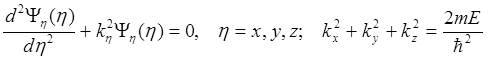         .   (2.10)

Рассмотрим уравнение для  Ψ_x(x) . Его частные решения имеют вид:

  .                                              (2.11)

Две волновые функции (2.11) являются как собственными функциями оператора Гамильтона, так и оператора импульса и соответствуют двум возможным состояниям частицы с одинаковой энергией и разным направлением проекции импульса:     p_x = ±ħk.  Общее решение можно представить в виде:

         .                                  (2.12)

В последнем случае импульс определен только по модулю |Р_x| = ħk.

Определяя две оставшиеся компоненты волновой функции выражениями аналогичными выражению (2.11) и умножая функцию (2.9) на временной множитель exp(-iEt/ħ), получим полную волновую функцию частицы с энергией Е и импульсом p в виде:

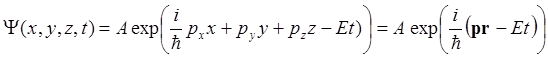.   (2.13)

Волновая функция свободной частицы имеет вид волны де-Бройля, частота и волновой вектор которой связан с импульсом и энергией частицы соотношениями p= ħk, Е=ħω.  Волновая функция (2.13) удовлетворяет всем стандартным условиям при любом значении энергии Е≥0, энергетический спектр частицы является непрерывным.

Квадрат модуля волновой функции вида (2.13) очевидно является константой. Это означает, что координаты частицы могут принимать любые значения с равной вероятностью. Волновую функцию частицы локализованной в определенной области пространства можно представить как суперпозицию волн де-Бройля – так называемый волновой пакет. Ограничимся одномерным случаем и рассмотрим суперпозицию волн де-Бройля, волновое число которых непрерывным образом меняется в интервале от k₀-Δk до k₀+Δk, где Δk – малая окрестность точки k₀:

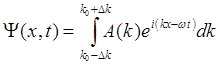               .                       (2.14)

Введём обозначение k-k₀=z  и полагая A(k)? A₀ проведём разложение функции  ω(k) по малому отклонению z, ограничившись двумя членами разложения:

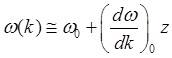.           (2.15)

Подставим выражение (2.15) в интеграл (2.14):

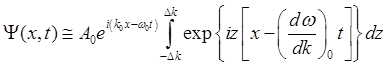     .           (2.16)

После вычисления интеграла окончательно получим:

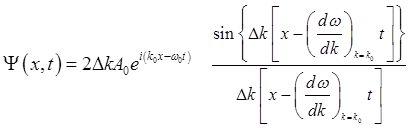                     (2.17)

При умножении волновой функции (2.17) на комплексно сопряжённую ей функцию Ψ^*(x,t) быстро осциллирующий экспоненциальный множитель исчезает, и распределение вероятности координаты частицы определяется квадратом функции

  , в которой

   .

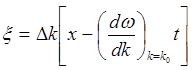График функции представлен на рис.3.

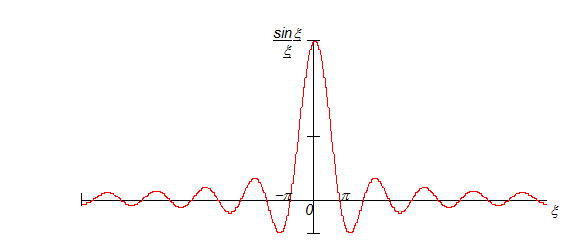
Рис.3. Волновой пакет.

Главный максимум функции находится в точке ξ=0, а координаты её узлов определяются условием  ξ=nπ, где n=1,2,3,… . При t=0 центр волнового пакета находится в точке x=0, а за его ширину можно принять область Δx, ограниченную точками xΔk=±π, откуда получим ΔxΔk=2π. Таким образом, чем больше разброс значений Δk волн де-Бройля, образующих волновой пакет, тем меньше ширина пакета. Умножая последнее равенство на постоянную Планка ħ, получим соотношение, связывающее размер области, в которой локализована частица, с неопределённостью её импульса:

ΔxΔp_x=2πħ  .

Положение максимума волнового пакета определяет наиболее вероятную координату частицы. Как следует из формулы (2.17), этот максимум движется со скоростью

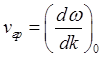  ,                                  которая называется групповой скоростью волн де-Бройля. Принимая во внимание, что для свободной частицы

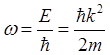                                     (2.18)

получим

   .

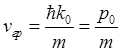Скорость движения максимума волнового пакета равна средней скорости частицы.

В процессе движения форма волнового пакета (2.17) не меняется, что обусловлено приближенным характером зависимости ω от k в разложении

(2.15).  Учёт следующего члена разложения приводит к «расплыванию» волнового пакета со временем. Для того, чтобы убедиться в этом рассмотрим волновой пакет вида 

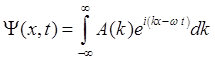                            ,                       (2.19)

где 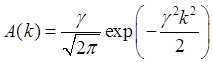                                 .                       (2.20)

Воспользовавшись известным интегралом

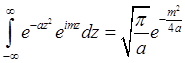             , подставляя (2.18) и (2.20) в (2.19) получим        

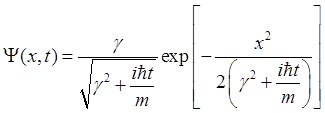      и 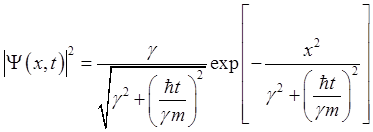                 .           (2.21)

Как видно из полученного выражения волновой пакет представляет собой распределение Гаусса (рис.4).

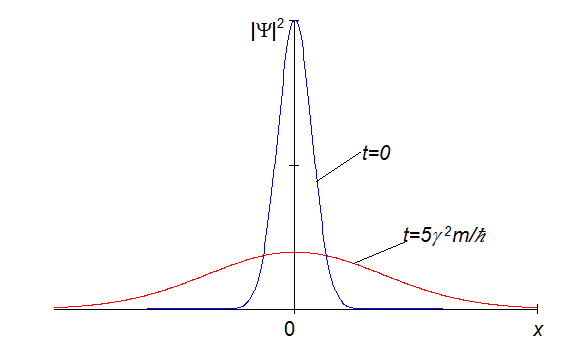
Рис.4. Расплывание волнового пакета со временем.

Максимум пакета покоится в точке 0. В начальный момент времени t=0  ширина пакета определяется параметром γ. С течением времени его ширина Г(t) растет по закону

.                                                         

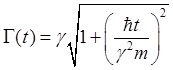Так, если электрон первоначально локализован в области, линейный размер которой  равен 10^-8см, то за время порядка 10^-16с эта область увеличится в два раза. Для того, чтобы наблюдать изменение этого пакета за время 10^-15с щёлкните два раза левой кнопкой мыши на расположенном выше значке.