Решение рациональных уравнений. Решение иррациональных уравнений. Числовые последовательности. Свойства числовых неравенств. Квадратичное неравенство. Решение квадратичных неравенств

РЕШЕНИЕ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ.

Уравнение вида , где - некоторые числа, называется рациональным. В случае, когда  или , получаем линейное и, соответственно, квадратное уравнения. Если  , то рациональное уравнение решается разложением на множители многочлена . Это осуществляется либо методом группировки, либо с помощью следующего утверждения.

Теорема Безу. Если - корни многочлена , то многочлен  делится на произведение .

Из теоремы Безу следует, что для разложения на множители многочлена достаточно найти некоторые его корни.

Если коэффициенты уравнения являются целыми числами, то в некоторых случаях корни можно подобрать исходя из их вида.

Теорема о целых корнях. Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена .

Из теоремы следует, что при отыскании целых корней многочлена с целыми коэффициентами достаточно проверить все делители свободного члена.

Теорема о дробных корнях. Если многочлен имеет рациональный корень , то числитель является делителем свободного члена , а знаменатель - делителем коэффициентапри старшей степени .

     Пример 1. Решить уравнение

.

Решение. Проверим уравнение на существование целых корней. Для этого найдём все делители свободного коэффициента, т. е. числа 50. Это  Подставляя поочерёдно эти значения вместо переменной в наше уравнение, находим первый корень . По теореме Безу левая часть имеет множитель . Разделив многочлен   на  (например уголком), получаем

Рассматривая теперь уравнение , и проверяя делители числа 25, убеждаемся в том, что целых корней больше нет. По теореме о дробных корнях проверяем всевозможные дроби, в которых знаменатель – делитель коэффициента при , т. е. числа 3, числитель – делитель числа 25. Это 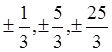. Проверкой убеждаемся, что  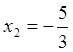- корень нашего уравнения. По теореме Безу выражение  делится на . Выполнив деление, получаем

.

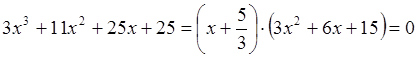Решая квадратное уравнение , находим остальные корни 

.

Ответ: .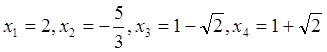

В некоторых случаях удаётся понизить степень уравнения с помощью подстановок.

Пример 2. Решить уравнение .

Решение. Разделим уравнение на . Получим

.

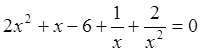Сгруппируем

.

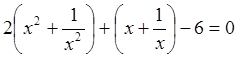Сделаем замену 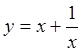. Тогда 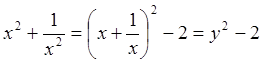. В результате получим уравнение  или . Решая которое, находим 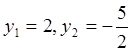. Отсюда 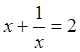, . Приравняв 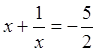, получим .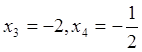

РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ.

     Определение. Уравнение, содержащее переменную под знаком радикала (корня), называется иррациональным.

Для решения иррациональных уравнений в простейших случаях могут быть использованы: метод приведения к смешанной системе уравнений и неравенств, метод замены переменной, метод возведения обеих частей в некоторую степень.

Иррациональное уравнение с корнем чётной степени  равносильно системе

 

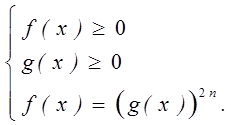
Это значит, чтобы решить исходное уравнение, необходимо найти корни уравнения и проверить, удовлетворяют ли они условиям  В некоторых случаях целесообразно начинать с проверки выполнения этих условий.

Иррациональное уравнение с корнем нечётной степени  равносильно уравнению . Рассмотрим схемы решения иррациональных уравнений других видов.

    

Данное уравнение равносильно системе

.

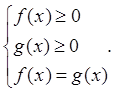
Это уравнение решается составлением совокупности систем

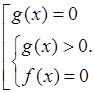
Решение данного уравнения осуществляется с помощью системы

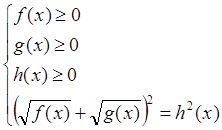
Затем уравнение сводится к одному из перечисленных выше видов.

Данное уравнение преобразуется сначала к виду

, затем составляется система

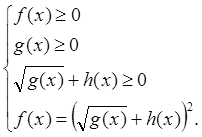
Уравнение вида  решается составлением равносильной системы

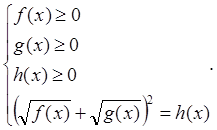
Уравнение  преобразовывается к уравнению , которое имеет только что рассмотренный вид.    

Метод возведения в степень состоит в том, что, оставляя некоторый радикал в одной части уравнения, возводят обе части уравнения в соответствующую степень. Так продолжают до тех пор, пока не получат уравнение, не содержащее радикалов. Так как при этом могут появиться посторонние корни, то необходимо сделать проверку найденных корней. Проверка обязательна и при введении новой переменной в методе подстановки.

ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ.

     Числовой последовательностью, или последовательностью, называют числовую функцию,

, определённую на множестве всех натуральных чисел .  Числовую последовательность называют конечной, если она определена на конечном подмножестве натуральных чисел: , , и бесконечной, если она определена на бесконечном подмножестве всех натуральных чисел: , . Числа , называются, соответственно, первым, вторым, третьим,…, - м, … членами последовательности, а сами значения аргументов – , - номерами членов последовательности. Член  называют общим членом последовательности.

Пример. Если , то .

Последовательность называют возрастающей, если всегда , и - убывающей, если , для любого натурального числа .

Последовательность называют неубывающей, если , и невозрастающей, если . Невозрастающие и неубывающие последовательности называются монотонными. Последовательность  называется ограниченной сверху, если существует такое число , что , для любого номера . Последовательность  называется ограниченной снизу, если существует такое число , что , для любого номера . Ограниченные сверху и снизу последовательности, называются просто