Прохождение частицы через потенциальный барьер. Коэффициенты прохождения и отражения. Прозрачность прямоугольного барьера. Барьер произвольной формы

Лекция № 11.

Прохождение частицы через потенциальный барьер.

Ключевые слова:

коэффициенты прохождения и отражения прозрачность прямоугольного барьера барьер произвольной формы

Обратимся к потенциальному барьеру изображенному на рис.2. Вдали от силового центра, где частица является свободной, её состояние, соответствующее движению с определенным импульсом, описывается волной де-Бройля. Пусть частица с импульсом p и энергией Е падает на барьер из минус бесконечности. Общее решение стационарного уравнения Шредингера на минус бесконечности можно представить в виде:

  .                 (2.53)

Первое слагаемое в этом выражении Ψ_пад(x) описывает  частицу с импульсом p=ћk, падающую на барьер, тогда как второе слагаемое Ψ_отр(x), очевидно, следует отождествить с частицей отраженной от барьера и движущейся в противоположном направлении.  На плюс бесконечности, при условии падения частицы на барьер слева, может находиться лишь частица, прошедшая барьер и движущаяся в положительном направлении оси х. Поэтому, соответствующая волновая функция имеет вид:

 .                                               (2.54)

Определим коэффициенты прохождения D и отражения частицы R выражениями:

,                                  (2.55)

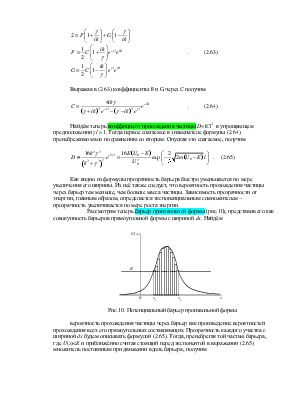
где  j  с соответствующими индексами – вектора плотности тока вероятности  падающей, прошедшей и отраженной частицы. Подставляя волновые функции в выражение для плотности тока вероятности, которое в одномерном случае имеет вид

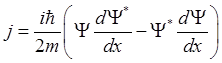        , получим:

     ,              ,                       .

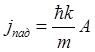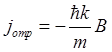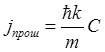Подставляя полученные выражения в формулы (2.55) и полагая коэффициент А в падающей волне равным 1, окончательно получим

                                                        (2.56)

В качестве примера найдём прозрачность прямоугольного барьера, изображённого на рис.9. Разбивая числовую ось на три отдельные области,

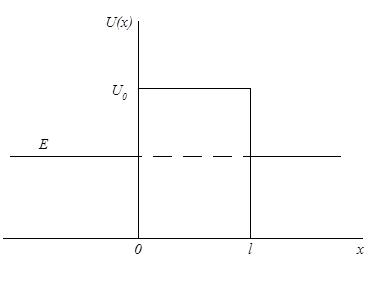
Рис.9. Прямоугольный потенциальный барьер получим для каждой из них уравнение Шредингера в виде

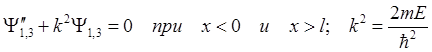                    (2.57)

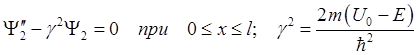           .           (2.58)

Пусть частица падает на барьер слева. Тогда, с учётом сказанного выше, для волновой функции слева и справа от барьера получим

                 (2.59)                                    

               .           (2.60)

Решение во второй области имеет вид

         .           (2.61)

Коэффициенты в волновых функциях найдём из граничных условий

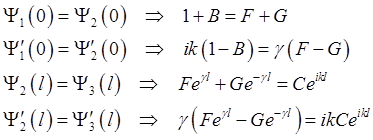                    (2.62)

Исключая из первых двух уравнений В, а с помощью двух последних выражая F и G через C, получим

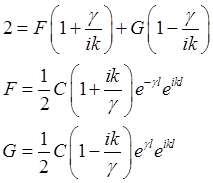                                        .           (2.63)

Выражая в (2.63) коэффициенты F и G через С получим

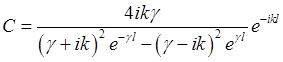                          .           (2.64)

Найдём теперь коэффициент прохождения частицы D=‌‌‌‌‌‌|C|²   в упрощающем предположении γl » 1. Тогда первое слагаемое в знаменателе формулы (2.64) пренебрежимо мало по сравнению со вторым. Опуская это слагаемое, получим

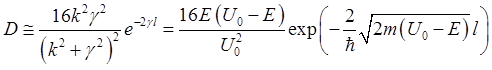  .     (2.65)

Как видно из формулы прозрачность барьера быстро уменьшается по мере увеличения его ширины. Из неё также следует, что вероятность прохождения частицы через барьер тем меньше, чем больше масса частицы. Зависимость прозрачности от энергии, главным образом, определяется экспоненциальным сомножителем – прозрачность увеличивается по мере роста энергии.

Рассмотрим теперь барьер произвольной формы (рис.10), представив его как совокупность барьеров прямоугольной формы с шириной dx. Найдём

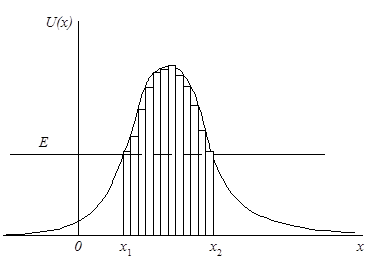
Рис.10. Потенциальный барьер произвольной формы вероятность прохождения частицы через барьер как произведение вероятностей прохождения всех его прямоугольных составляющих. Прозрачность каждого участка с шириной dx будем описывать формулой (2.65). Тогда, пренебрегая той частью барьера, где U(x)<E и приближённо считая стоящий перед экспонентой в выражении (2.65) множитель постоянным при движении вдоль барьера, получим

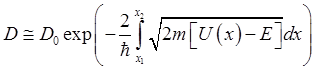        ,                       (2.66)  где коэффициент D₀ слабо зависит от энергии частицы и может считаться постоянным.

Рассмотренный выше туннельный эффект лежит в основе ряда физических явлений таких, как: контактная разность потенциалов, холодная эмиссия электронов из металла, альфа распад и т.д.