этому уравнению, являются координатами некоторой точки фигуры.
Определение. Окружностьюназывается фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки. Эта точка называется центром окружности. Расстояние от точек окружности до её центра называется радиусом окружности.Радиусом называется также любой отрезок, соединяющий точку окружности с её центром.
Выведем уравнение окружности
с центром в точке ![]() и радиусом
и радиусом ![]() (рис. 12).
(рис. 12).
|
|
Возьмём произвольную точку ![]() на окружности. Расстояние от неё до центра
на окружности. Расстояние от неё до центра
![]() равно
равно ![]() .
Квадрат расстояния от точки
.
Квадрат расстояния от точки ![]() до
до ![]() равен
равен
![]() .
.
Таким образом, координаты ![]() и
и ![]() каждой
точки
каждой
точки ![]() окружности удовлетворяют уравнению
окружности удовлетворяют уравнению
![]() . (2)
. (2)
Обратно: любая точка ![]() , координаты которой удовлетворяют
уравнению (2), принадлежит окружности, так как расстояние от неё до точки
, координаты которой удовлетворяют
уравнению (2), принадлежит окружности, так как расстояние от неё до точки ![]() равно
равно ![]() . Отсюда
следует, что уравнение (2) действительно является уравнением окружности с
центром
. Отсюда
следует, что уравнение (2) действительно является уравнением окружности с
центром ![]() и радиусом
и радиусом ![]() .
Заметим, что если центром окружности является начало координат, то уравнение
окружности имеет вид:
.
Заметим, что если центром окружности является начало координат, то уравнение
окружности имеет вид:
![]() .
.
ОПРЕДЕЛЕНИЕ
И СВОЙСТВА ФУНКЦИИ ![]() И ЕЁ ГРАФИК.
И ЕЁ ГРАФИК.
|
Определение.
Функция вида |
Постоянная функция и прямая пропорциональность - частные случаи линейной функции.
1. Область определения функции - множество всех
действительных чисел ![]() .
.
2. Область значений функции при ![]() - множество
- множество ![]() и - {
и - {![]() }, если
}, если ![]() = 0.
= 0.
Действительно, уравнение ![]() , если
, если ![]() ¹
0, имеет решение при любом
¹
0, имеет решение при любом ![]() , следовательно,
выражение
, следовательно,
выражение ![]() принимает в этом случае любое значение.
принимает в этом случае любое значение.
Если же![]() , то
, то ![]() для любого значения
для любого значения ![]() .
.
3. Корни функции ![]() :
: 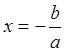 .
.
4. Промежутки постоянного знака:
а) если ![]() , то
функция положительна
, то
функция положительна ![]() при
при 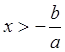 и
отрицательна при
и
отрицательна при 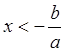 ;
;
б) если ![]() , то
функция положительна
, то
функция положительна ![]() , при
, при 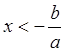 и
отрицательна при
и
отрицательна при 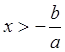 .
.
5. Промежутки монотонности:
а) если ![]() , то
функция возрастает, т. к. из
, то
функция возрастает, т. к. из ![]() следует
следует ![]() и
и ![]() , т.е.
, т.е. ![]() ;
;
б) если ![]() , то
функция убывает, т.к. из
, то
функция убывает, т.к. из ![]() следует
следует ![]() и
и ![]() , т.е.
, т.е. ![]() .
.
6. При ![]() и
и ![]() функция
функция ![]() ни
чётная ни нечётная, так как
ни
чётная ни нечётная, так как ![]() и
и ![]() .
.
При ![]() функция
функция
![]() принимает вид
принимает вид ![]() и
является нечётной, так как
и
является нечётной, так как ![]() .
.
При ![]() функция
функция
![]() принимает вид
принимает вид ![]() и
является чётной, так как
и
является чётной, так как ![]() .
.
7. При ![]() функция
функция ![]() непериодична,
так как для любого
непериодична,
так как для любого ![]()
![]() .
.
Теорема. Графиком
линейной функции ![]() является прямая.
является прямая.
Доказательство. Будем
рассматривать случаи ![]() и
и ![]() одновременно
(рис. 13). Проведём прямую
одновременно
(рис. 13). Проведём прямую ![]() через точки с
координатами
через точки с
координатами ![]() и
и ![]() , причём
, причём
![]() . Покажем, что эта прямая является графиком
функции
. Покажем, что эта прямая является графиком
функции ![]() . Для этого возьмём
. Для этого возьмём 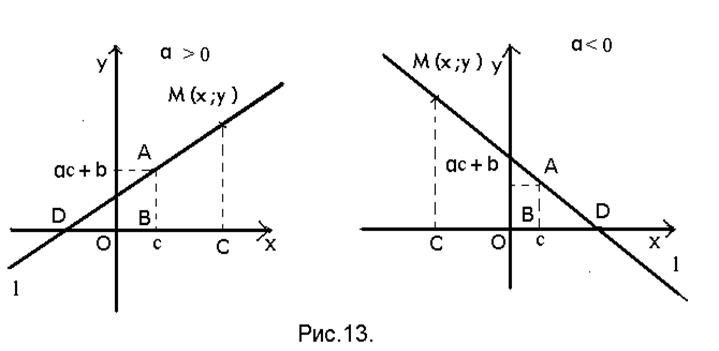 произвольную точку
произвольную точку ![]() , лежащую на прямой
, лежащую на прямой ![]() .
Из подобия треугольников
.
Из подобия треугольников ![]() и
и ![]() заключаем, что
заключаем, что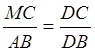 . Учитывая,
что
. Учитывая,
что ![]() ,
, ![]() ,
, 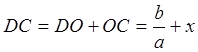 ,
, 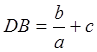 , имеем
, имеем
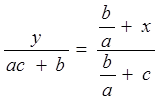 .
.
Это равносильно тому, что
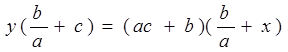
или
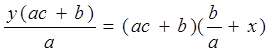 .
.
Сократив это равенство на ![]() ,
получим
,
получим
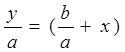 , или
, или ![]() . Итак, все точки
прямой
. Итак, все точки
прямой ![]() с координатами
с координатами ![]() удовлетворяют уравнению
удовлетворяют уравнению ![]() .
.
С другой стороны, если точка ![]() не
лежит на прямой
не
лежит на прямой ![]() , то справедливо либо неравенство
, то справедливо либо неравенство
![]() >
> ![]() (точка
лежит выше прямой), либо
(точка
лежит выше прямой), либо ![]() <
< ![]() (точка лежит ниже прямой).
(точка лежит ниже прямой).
Этим мы показали, что
координаты точек прямой ![]() и только они
удовлетворяют уравнению
и только они
удовлетворяют уравнению![]() . Теорема доказана.
. Теорема доказана.
ОПРЕДЕЛЕНИЕ И
СВОЙСТВА ФУНКЦИИ 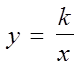 (ГДЕ
(ГДЕ ![]() ) И ЕЁ ГРАФИК.
) И ЕЁ ГРАФИК.
Определение. Функция,
которая задаётся формулой 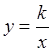 , где
, где ![]() , называется обратной
пропорциональностью.
, называется обратной
пропорциональностью.
Свойства функции 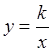 , где
, где ![]() .
.
1. Область определения:
![]() .
.
2. Область значений: ![]() .
.
Действительно, для любого ![]() ,
найдётся такое значение
,
найдётся такое значение![]() , что
, что 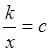 . Это
значение
. Это
значение 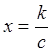 . Если же
. Если же ![]() , то
, то 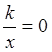 , откуда
, откуда ![]() , что
противоречит условию
, что
противоречит условию ![]() .
.
3. Чётность, нечётность.
Функция нечётна при любом ![]() , так как для любого
, так как для любого
![]() ,
, 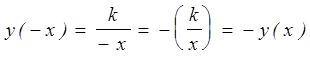 .
.
Следовательно, график функции симметричен относительно начала координат.
4. Периодичность. Функция непериодическая. Действительно, если
бы существовало ![]() такое, что для всех
такое, что для всех ![]() , то, взяв
, то, взяв ![]() , имели
бы
, имели
бы ![]() , что невозможно, так как
, что невозможно, так как ![]() .
.
4. Точек пересечения с
осями нет, так как ![]() .
.
5. Промежутки
знакопостоянства. Если ![]() , то
, то 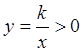 при
при ![]() и
и ![]() при
при ![]() . Таким
образом, график лежит в первой и третьей координатных четвертях.
. Таким
образом, график лежит в первой и третьей координатных четвертях.
Если ![]() , то
, то ![]() > 0 при
> 0 при ![]() и
и ![]() при
при ![]() , т. е.
график расположен во второй и четвёртой координатных четвертях.
, т. е.
график расположен во второй и четвёртой координатных четвертях.
6. Промежутки монотонности
и экстремумы. Функция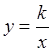 при
при ![]() убывает в каждом из промежутков
убывает в каждом из промежутков ![]() и
и ![]() .
Действительно, пусть, например,
.
Действительно, пусть, например, ![]() . Тогда
. Тогда
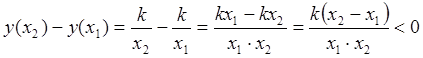 , а,
следовательно,
, а,
следовательно, ![]() , т. е. в промежутке
, т. е. в промежутке ![]() функция
функция 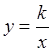 при
при ![]() убывает. Аналогично можно показать
убывание функции и для промежутка
убывает. Аналогично можно показать
убывание функции и для промежутка ![]() .
.
Нетрудно
убедиться, что функция 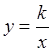 при
при ![]() возрастает в каждом из промежутков
возрастает в каждом из промежутков ![]() и
и ![]() .
Заметим, что в этих случаях функция
.
Заметим, что в этих случаях функция 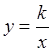 не является убывающей
(или возрастающей) на всей области определения.
не является убывающей
(или возрастающей) на всей области определения.
7. Графиком функции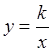 является
гипербола. Она состоит из двух ветвей, симметричных относительно начала
координат.
является
гипербола. Она состоит из двух ветвей, симметричных относительно начала
координат.
При значениях ![]() , стремящихся к нулю,
значения функции
, стремящихся к нулю,
значения функции 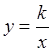 неограниченно возрастают
(по модулю). Поэтому прямая
неограниченно возрастают
(по модулю). Поэтому прямая ![]() (ось координат)
является вертикальной асимптотой графика функции
(ось координат)
является вертикальной асимптотой графика функции 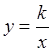 .
.
|
|
При ![]() значения функции
значения функции 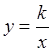 становятся сколь угодно малыми по
модулю, т. е. график приближается к оси абсцисс, но не пересекает и не касается
её. Поэтому прямая
становятся сколь угодно малыми по
модулю, т. е. график приближается к оси абсцисс, но не пересекает и не касается
её. Поэтому прямая ![]() (ось абсцисс) является горизонтальной
асимптотой графика (рис.14).
(ось абсцисс) является горизонтальной
асимптотой графика (рис.14).
ОПРЕДЕЛЕНИЕ
И СВОЙСТВА ФУНКЦИИ ![]() (ГДЕ
(ГДЕ ![]() ) И ЕЁ
ГРАФИК.
) И ЕЁ
ГРАФИК.
Определение. Функция
вида ![]()
![]() называется
квадратичной.
называется
квадратичной.
Свойства квадратичной функции.
1. Область определения:
![]() .
.
2. Область значений: Выполним преобразования
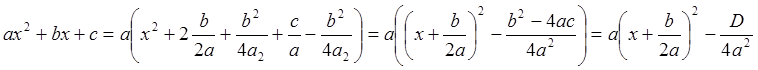 , где
, где![]() - дискриминант.
- дискриминант.
Так как 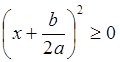 , то при
, то при ![]()
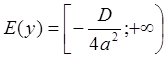 , а при
, а при ![]()
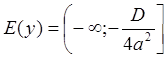 .
.
3. Чётность и нечётность.
При ![]() функция чётная, так как
функция чётная, так как ![]() и
и ![]() . При
. При ![]() функция не является чётной. Если
предположим, что функция чётная, то
функция не является чётной. Если
предположим, что функция чётная, то ![]() , т. е.
, т. е. ![]() , или
, или ![]() , что
равносильно
, что
равносильно ![]() при всех
при всех ![]() , откуда
, откуда
![]() , противоречие.
, противоречие.
Функция ![]() не является нечётной, так как из
равенства
не является нечётной, так как из
равенства
![]() , т. е.
, т. е. ![]() ,
при
,
при ![]() имеем
имеем ![]() , т. е.
, т. е. ![]() ; при
; при ![]()
![]() , т. е.
, т. е. ![]() , откуда
, откуда
![]() , что невозможно.
, что невозможно.
4. Функция непериодическая.
Предположим, что существует ![]() такое, что
такое, что
![]() , где
, где ![]() ,
, ![]() ,
, ![]() принадлежат
принадлежат
![]() .
.
Возьмём 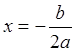 . Тогда из условия периодичности следует
. Тогда из условия периодичности следует
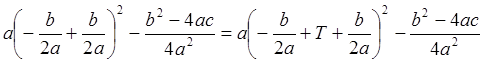 , откуда
, откуда ![]() .
.
Так как ![]() , то
, то ![]() .
Противоречие.
.
Противоречие.
5. Точки пересечения с
осями координат. С осью ![]() (нули функции), по формулам корней
квадратного уравнения: если
(нули функции), по формулам корней
квадратного уравнения: если ![]() , то две точки пересечения
, то две точки пересечения
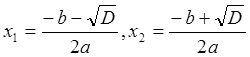 ;
;
если ![]() , то одна точка пересечения
, то одна точка пересечения 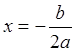 ;
;
если ![]() , то точек пересечения нет.
, то точек пересечения нет.
С осью ![]() : при
: при ![]() ,
, ![]() , т. е.
, т. е. ![]() .
.
6. Промежутки
знакопостоянства. Для определения знаков функции достаточно решить
квадратные неравенства ![]() или
или ![]() .
.
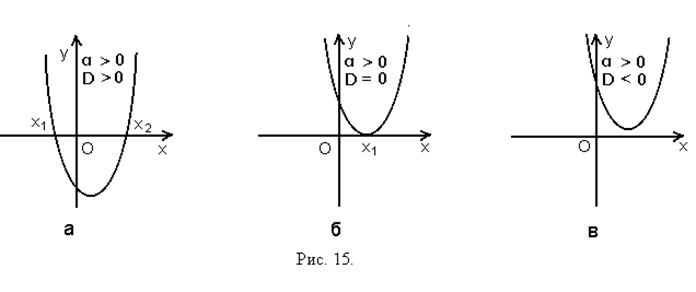
6.1 Если ![]() ,
, ![]() , то на
, то на ![]() функция положительна, а на
функция положительна, а на ![]() - отрицательна (рис.15.а).
- отрицательна (рис.15.а).
6.2.Если ![]() ,
, ![]() , то на
, то на
![]() функция положительна (рис.15.б).
функция положительна (рис.15.б).
6.3. Если ![]() ,
, ![]() , то
функция положительна на всей числовой оси (рис. 15.в).
, то
функция положительна на всей числовой оси (рис. 15.в).
 6.4. Если
6.4. Если ![]() ,
, ![]() , то на
, то на ![]() функция положительна, а на
функция положительна, а на ![]() отрицательна (рис.16.а).
отрицательна (рис.16.а).
6.5. Если ![]() ,
, ![]() , то на
, то на
![]() функция отрицательна (рис.16.б).
функция отрицательна (рис.16.б).
6.6.Если ![]() ,
, ![]() , то
функция отрицательна на
, то
функция отрицательна на ![]() (рис.16.в).
(рис.16.в).
|
|
7. Промежутки
монотонности. Если ![]() то функция
то функция ![]() убывает при
убывает при 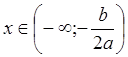 и
возрастает при
и
возрастает при 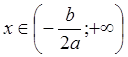 . Покажем, например, возрастание
функции на втором промежутке. Действительно, пусть
. Покажем, например, возрастание
функции на втором промежутке. Действительно, пусть 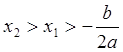 .
Тогда
.
Тогда 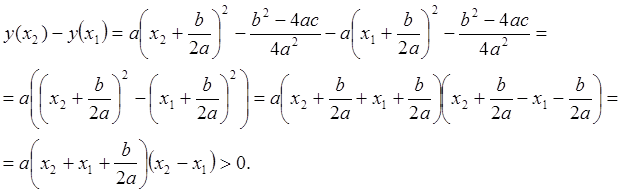
Так как при 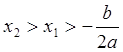 выражение
выражение 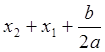 положительно.
положительно.
Если ![]() то
функция
то
функция ![]() возрастает при
возрастает при 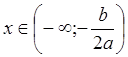 и
убывает при
и
убывает при 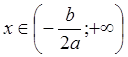 . Доказательство аналогично.
. Доказательство аналогично.
8. Графиком функции![]() является парабола с вершиной в точке
является парабола с вершиной в точке 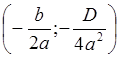 . Парабола получается из графика функции
. Парабола получается из графика функции ![]() путём сдвига вдоль оси
путём сдвига вдоль оси ![]() на
на 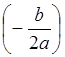 единиц
(вправо, если
единиц
(вправо, если 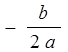 >
0 , и влево, если
>
0 , и влево, если 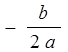 <
0) и последующего сдвига вдоль оси
<
0) и последующего сдвига вдоль оси ![]() на
на 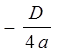 единиц (вверх, если
единиц (вверх, если 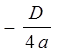 >
0, и вниз, если
>
0, и вниз, если 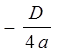 <
0). Осью симметрии является прямая
<
0). Осью симметрии является прямая 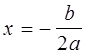 .
.
Варианты графиков представлены на рисунках 15 - 16.
СВОЙСТВА ФУНКЦИИ ![]() И ЕЁ ГРАФИК.
И ЕЁ ГРАФИК.
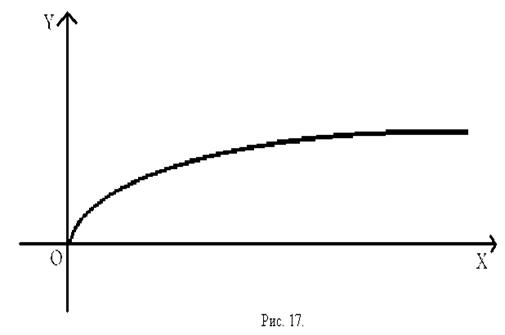 На множестве
На множестве ![]() функции
функции ![]() и
и
![]() являются взаимно обратными. Рассмотрим
более подробно свойства функции.
являются взаимно обратными. Рассмотрим
более подробно свойства функции.
1. Область определения: ![]() .
.
2. Область значений: ![]() .
.
3. Функция не является чётной и не является нечётной, так как область её определения не является симметричным множеством.
4. Функция непериодическая, так как область определения - непериодическое множество.
5. Функция возрастает на всей области своего определения.
Действительно, функция ![]() является обратной
на этом промежутке
является обратной
на этом промежутке
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.