Основные положения квантовой механики. Особенности поведения микрочастиц. Волновая функция. Принцип суперпозиции состояний, страница 2

Волновая функция.

Обратимся теперь к вопросу о способе задания состояния системы в квантовой механике. В классической механике состояние системы определяется, как известно, заданием совокупности координат и импульсов всех её частей. Такой способ определения состояния непригоден для микрообъектов в силу принципа неопределённости, сформулированного выше.

В основе квантовой механики лежит утверждение о том, что поведение системы полностью определяется заданием в некоторый момент времени комплексной функции координат, которая называется волновой функцией. Для системы, состоящей из одной частицы, в момент времени t=t₀ задаётся волновая функция Ψ(r), где r – радиус-вектор частицы. Волновая функция не может быть непосредственно измерена. Квадрат же её модуля имеет простой физический смысл: он пропорционален плотности вероятности обнаружения частицы в данной точке пространства:  . На волновую функцию налагаются, так называемые, стандартные условия, в соответствии с которыми она должна быть всюду непрерывной, однозначной, а также конечной за исключением, быть может, некоторых особых точек. Волновая функция определена с точностью до произвольного постоянного множителя. Это означает, что волновые функции  Ψ(r) и Ψ′(r)=CΨ(r), где С- произвольная константа, описывают одно и тоже состояние частицы. Будем также считать волновую функцию квадратично интегрируемой; случаи, когда это условие не выполняется, мы особо рассмотрим в дальнейшем. Как правило, волновую функцию интегрально нормируют на единицу:

            .                           (1.1)

Условие нормировки (1.1) отражает тот очевидный факт, что вероятность найти частицу где-либо в пространстве равна 1. Для нормированной таким образом волновой функции имеет место равенство . При этом волновая функция всё ещё определена с точностью до фазового множителя вида е^iα , где α – произвольное действительное число.

Описанный выше способ задания состояния в квантовой механике подразумевает, что волновая функция в любой произвольный момент времени t может быть определена по функции заданной в начальный момент времени t₀. Это является выражением принципа причинности в квантовой механике, в соответствии с которым заданное начальное состояние системы определяет её состояния в произвольный момент времени. В соответствии с этим волновую функцию следует считать зависящей не только от r, но и от времени . Временнáя зависимость волновой функции будет рассмотрена позже, при обсуждении основного уравнения динамики.

Для одномерного случая, когда частица может двигаться только вдоль оси х, условие нормировки (1.1) приобретает вид

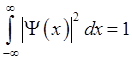                         (1.2)

Стоящее под интегралом выражение  определяет вероятность пребывания частицы в интервале значений координаты от х до х+dх. Умножая это выражение на координату, и интегрируя по всей числовой оси, получим среднее значение координаты :

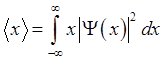          .                  (1.3)

Аналогично, для  имеем:

    .                 (1.4)

Волновая функция системы частиц зависит от координат всех составляющих её частей. В частности для системы из двух частиц получим функцию Ψ(r₁,r₂). Если частицы не взаимодействуют, её можно представить в виде произведения волновых функций отдельных частиц:

     .           (1.5)

Таким образом, плотность вероятности сложного события, состоящего в том, что первая частица находится в точке r₁, а вторая в точке r₂, равна произведению плотностей вероятности отдельных независимых событий, как и следует из теории вероятности.

Принцип суперпозиции состояний.

В предыдущей лекции появление дифракционных максимумов и минимумов при рассеянии микрочастиц на кристаллической решётке было объяснено интерференцией волн де-Бройля. Этот пример является частным проявлением одного из важнейших положений квантовой механики – принципа суперпозиции состояний.  Согласно этому принципу, если существуют состояния системы, которые описываются волновыми функциями Ψ₁ и Ψ₂, то существует состояние, которое описывается линейной комбинацией этих функций:

                                                 (1.6)

где С₁ и С₂ произвольные комплексные числа. Волновые функции в последнем выражении могут быть функциями одних только координат, или зависеть также от времени. При этом если в состоянии Ψ₁ некоторая наблюдаемая (можно говорить и о полном наборе наблюдаемых) имеет определённое значение F₁, а в состоянии Ψ₂ – определённое значение F₂, то в состоянии Ψ она принимает значения либо F₁ либо F₂. Вероятность получения этих значений, очевидно, зависит от коэффициентов С₁ и С₂. Это хорошо видно на примере, когда один из коэффициентов, например С₁ обращается в 0. Как мы вскоре убедимся, вероятности получения значений F₁ и F₂ равны соответственно |С₁|² и |С₂|² при условии, что |С₁|²+|С₂|²=1.

Добавим теперь к уже рассмотренным состояниям ещё одно - с волновой функцией Ψ₃. Рассмотрим его суперпозицию с состоянием, которое описывается волновой функцией Ψ вида (1.6). Действуя последовательно таким образом можно распространить принцип суперпозиции на случай трёх и более комбинирующих состояний. В общем случае, если известны волновые функции Ψ_k (где k=1,2, …) всех состояний, в которых наблюдаемая F имеет определённое значение, волновая функция произвольного состояния системы может быть представлена в виде

                                                   (1.7).

Из принципа суперпозиции вытекает линейность всех уравнений квантовой механики.