Основные математические понятия, факты, формулы и теоремы. Натуральные числа. Простые и составные числа. Делитель, кратное. Наибольший общий делитель, наименьшее общее кратное. Степень с натуральным и целым показателями. Свойства степеней с натуральным и целым показателями

Натуральные числа, противоположные им числа и нуль называют целыми числами. Множество всех целых чисел обозначают :

.

Сложение целых чисел подчинено переместительному (коммутативному) и сочетательному (ассоциативному) законам, выражаемым соответственно равенствами:

1)  

2)   , для любых целых чисел , , .

Умножение целых чисел также обладает переместительным и сочетательным свойствами, выражаемыми для любых значений , ,  соответственно равенствами:

3)  

4)  

При любых значениях , ,  выполняется равенство :

5)  

Это свойство выражает распределительный закон умножения относительно сложения. Введение отрицательных чисел делает выполнимым действие вычитания над целыми числами (разность имеет смысл и при < ). Арифметические действия над целыми числами выполняют по правилам, приведённым ниже.

1.   Чтобы сложить два отрицательных числа, нужно сложить их модули и перед полученным числом поставить минус. Например, .

2.   Чтобы сложить два числа с разными знаками, надо из большего модуля вычесть меньший и поставить перед полученным числом знак того слагаемого, модуль которого больше. Например, ;

;

;

.

Сумма противоположных чисел всегда равна нулю.

3.   Если надо сложить несколько чисел, среди которых есть положительные и отрицательные, можно сложить отдельно положительные и отдельно отрицательные, а потом к сумме положительных чисел прибавить сумму отрицательных чисел. Например, 23 + 11 + (-10 ) + (-32 ) = 34 + (-42 ) = -8.

4.   Чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.

5.   Чтобы перемножить два числа с разными знаками, нужно перемножить модули этих чисел и перед полученным числом поставить минус.

6.   Чтобы перемножить два отрицательных числа, надо перемножить их модули. Произведение двух отрицательных чисел есть число положительное.

7.   Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя. Частное двух отрицательных чисел есть число положительное.

8.   Чтобы разделить два числа с разными знаками, надо разделить модуль делимого на модуль делителя и перед полученным числом поставить минус.

     РАЦИОНАЛЬНЫЕ ЧИСЛА. ДЕЙСТВИЯ НАД РАЦИОНАЛЬНЫМИ ЧИСЛАМИ. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ.

Рациональной дробью   называют упорядоченную пару целых чисел и , у которой  . В рациональной дроби  число  называют числителем, а число  - знаменателем.

Две рациональные дроби   и  называют равными или эквивалентными тогда и только тогда, когда , т. е.

.

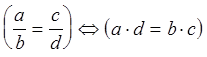Это соотношение эквивалентности обладает следующими свойствами :

1)   ;

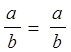2)   если 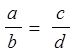, то ;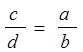

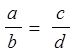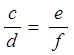3)   если  и , то .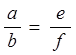

Первое свойство называют свойством рефлексивности, второе - свойством симметричности, третье - свойством транзитивности.

Рациональным числомназывают каждый класс эквивалентных рациональных дробей. Разные классы определяют разные рациональные числа. Для обозначения рационального числа  применяют рациональную дробь  из классаэквивалентности, задающего это число: 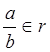. Таким образом, одно и то же рациональное число может быть записано разными, но эквивалентными дробями. Например, рациональное число можно записать каждой из рациональных дробей:

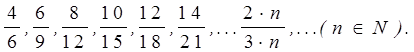
Множество рациональных чисел обозначают .

          Арифметические действия над рациональными числами определяются следующим образом:

Суммой рациональных дробей  и  называют рациональную дробь, определяемую формулой 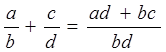 . Эта формула означает следующее:

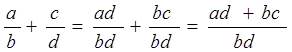, т. е. дроби с различными знаменателями приводятся к общему знаменателю