


Лекция №4.
План лекции:
операторы момента.
Ключевые слова:
коммутационные соотношения для операторов момента магнитное квантовое число орбитальное квантовое число собственные функции оператора момента
Операторы момента.
Операторы проекций момента определяются формулой (1.40) и имеют вид
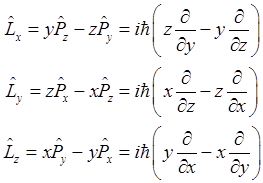 (1.50).
(1.50).
Наряду с операторами проекций, определим оператор квадрата момента
![]() (1.51).
(1.51).
Можно показать, что правила коммутации введённых операторов момента определяются выражениями
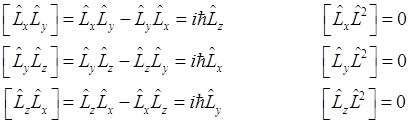 (1.52).
(1.52).
Из полученных коммутационных соотношений следует, что определённое значение в один и тот же момент времени могут иметь квадрат (модуль) момента и одна из его проекций. Вместе с тем какие-либо две проекции момента не могут быть определены одновременно.
Запишем теперь операторы ![]() и
и ![]() в
сферической системе координат, полярный угол которой
в
сферической системе координат, полярный угол которой ![]() будем отсчитывать как обычно от оси OZ, а угол
будем отсчитывать как обычно от оси OZ, а угол ![]() от оси OX. Оператор проекции момента имеет вид
от оси OX. Оператор проекции момента имеет вид
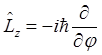 (1.53).
(1.53).
Найдём собственные функции и спектр собственных значений оператора. Собственные функции удовлетворяют уравнению
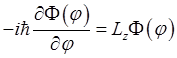 .
.
Решая уравнение, получим
![]() , где С – нормирующий множитель. Полученная функция
должна удовлетворять стандартным условиям. Одно из них, условие однозначности
функции приводит к требованию
, где С – нормирующий множитель. Полученная функция
должна удовлетворять стандартным условиям. Одно из них, условие однозначности
функции приводит к требованию
![]() . Это условие выполняется лишь в том
случае, если отношение
. Это условие выполняется лишь в том
случае, если отношение ![]() является целым числом.
Отсюда получаем
является целым числом.
Отсюда получаем
![]() (1.54), где квантовое число m
называется магнитным
квантовым числом. Для волновой функции получим
(1.54), где квантовое число m
называется магнитным
квантовым числом. Для волновой функции получим
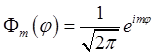 (1.55), причём она удовлетворяет условию ортонормированности
(1.55), причём она удовлетворяет условию ортонормированности
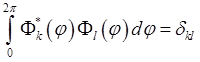 (1.56)
(1.56)
Обратимся теперь к оператору ![]() .
В сферической системе координат он имеет вид
.
В сферической системе координат он имеет вид
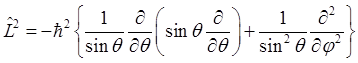 (1.57).
(1.57).
Найдём общие собственные функции операторов ![]() и
и ![]() .
Собственные функции и собственные значения оператора
.
Собственные функции и собственные значения оператора ![]() определятся из уравнения
определятся из уравнения
![]() (1.58), где
(1.58), где ![]() , а
, а ![]() - функция вида (1.55).
Введём вспомогательные операторы вида
- функция вида (1.55).
Введём вспомогательные операторы вида
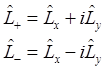 (1.59).
(1.59).
Определим правила коммутации введённых операторов с
оператором ![]() . Используя коммутационные
соотношения (1.52), получим
. Используя коммутационные
соотношения (1.52), получим
![]() (1.60).
(1.60).
Пусть ![]() - собственная
функция оператора
- собственная
функция оператора ![]() , принадлежащая
собственному значению
, принадлежащая
собственному значению ![]() . Тогда с учётом
соотношения (1.60) получим
. Тогда с учётом
соотношения (1.60) получим
![]() (1.61).
(1.61).
Из последнего соотношения вытекает, что стоящие в скобках
функции ![]() , также являются собственными
функциями оператора
, также являются собственными
функциями оператора ![]() , принадлежащими
значениям
, принадлежащими
значениям ![]() и
и ![]() соответственно.
Таким образом, оператор
соответственно.
Таким образом, оператор ![]() порождает, а
оператор
порождает, а
оператор ![]() уничтожает один квант момента.
уничтожает один квант момента.
Проекция момента не может быть больше его
модуля. Поэтому, при заданном значении ![]() магнитное
квантовое число ограничено по модулю. Пусть
магнитное
квантовое число ограничено по модулю. Пусть ![]() .
Поскольку состояние
.
Поскольку состояние ![]() не существует, то
не существует, то ![]() . Подействуем на это соотношение слева
оператором
. Подействуем на это соотношение слева
оператором ![]() . Тогда получим
. Тогда получим
![]() .
.
Из последнего равенства следует, что собственные значения квадрата момента определяются формулой
![]() (1.62),
(1.62),
где число l называется орбитальным квантовым числом.
С учётом последней формулы уравнение приобретает вид
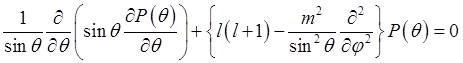 .
. ![]()
Это уравнение хорошо известно в математике. Его решения
представляют собой присоединённые полиномы Лежандра ![]() ,
которые определяются формулами
,
которые определяются формулами
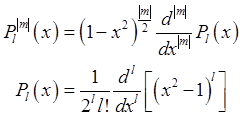 (1.63).
(1.63).
Собственные
функции оператора ![]() представляют
собой сферические функции
представляют
собой сферические функции
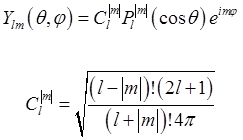 (1.64).
(1.64).
Функции вида (1.64) удовлетворяют условию ортонормированности
![]() (1.65), где интегрирование ведётся по полному телесному углу
(1.65), где интегрирование ведётся по полному телесному углу ![]() .
.
Состояния с определённым значением квадрата
момента импульса являются вырожденными по магнитному квантовому числу m, причём кратность вырождения равна 2l+1. Вырождение выражается в том, что одному собственному
значению модуля момента соответствует несколько (2l+1)
собственных функций ![]() , отличающихся квантовым
числом m. Это вырождение связано с тем, что
вектор момента при одном и том же значении его модуля, может быть различным
образом ориентирован по отношению к оси OZ.
, отличающихся квантовым
числом m. Это вырождение связано с тем, что
вектор момента при одном и том же значении его модуля, может быть различным
образом ориентирован по отношению к оси OZ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.