Одномерное движение. Общие свойства решений уравнения Шредингера

ГЛАВА 2.  ОДНОМЕРНОЕ   ДВИЖЕНИЕ

Лекция № 7.

Общие свойства решений уравнения Шредингера.

Ключевые слова:

энергетический спектр

туннельный эффект

эффект надбарьерного отражения

В этой главе рассматривается частный случай движения частицы с одной степенью свободы в потенциальном поле U(x). Рассмотрим сначала потенциальную функцию, которая имеет минимум и стремится к нулю на бесконечности, как показано на рис.1.

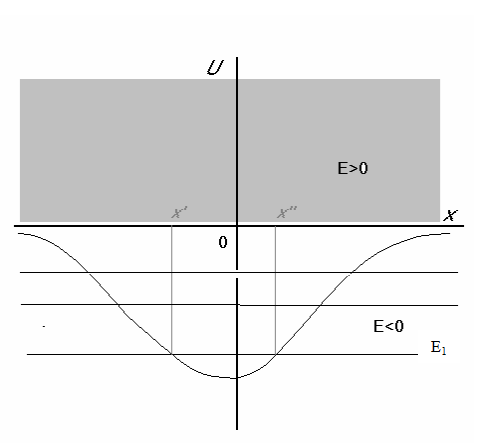
Рис.1. Потенциальная яма.

Энергетический спектр частицы расположен в области значений энергии больше, чем U_min. Это следует из цепи очевидных неравенств:

При Е<0 движение частицы является ограниченным (финитным). Действительно, в противном случае частица может уйти на бесконечность, где она является свободной. Но тогда она будет обладать только кинетической энергией, которая не может быть отрицательной. Энергетический спектр частицы  является дискретным, так как в состояниях с непрерывным спектром, как уже отмечалось в  предыдущей главе, частица находится на бесконечности.

При Е>0 движение частицы является неограниченным (инфинитным), а её энергетический спектр – непрерывным.

Понятия финитного и инфинитного в квантовой и классической механике отличаются. Квантовая частица с энергией Е₁ (рис.1) способна выходить за пределы области ограниченной поворотными точками x^/ и x^//, в которой может находиться классическая частица. Рассмотрим потенциальный барьер, изображенный на рис.2.

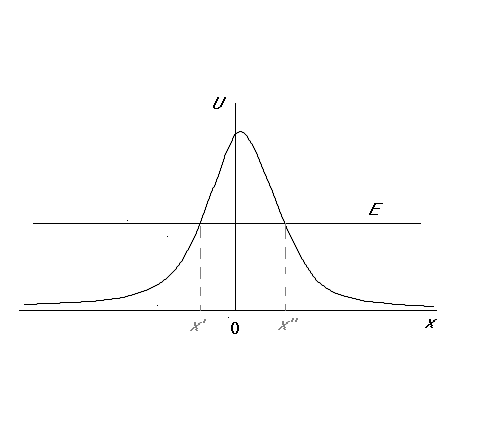
Рис.2. Потенциальный барьер.

Если полная энергия частицы Е меньше высоты потенциального барьера, то в классической механике область движения частицы разбивается на две несвязанные между собой области соответственно слева и справа от поворотных точек x’ и x’’. Действительно нахождение частицы на отрезке между точками x’ и x’’ означало бы, что её полная энергия меньше потенциальной, а кинетическая энергия отрицательна, что невозможно. Таким образом, частица не может преодолеть потенциальный барьер, её движение ограничено с одной стороны.

В квантовой механике вышеприведенные рассуждения оказываются неверными. Действительно из принципа неопределенности следует, что из трех величин: полной, кинетической и потенциальной энергии определенное значение в данный момент времени может иметь только одна. В стационарном состоянии координата частицы не имеет определенного значения, частицы с некоторой вероятностью может находиться и в области запретной для классического движения. Обнаружение частицы в этой области не противоречит закону сохранения энергии, т.к. локализация частицы внутри отрезка, ограниченного точками x’ и x’’ приведёт к тому, что её энергия уже не будет иметь определенного значения. Из сказанного ясно, что в квантовой механике частица, энергия которой меньше высоты потенциального барьера, может пройти через барьер и уйти на бесконечность – её движение оказывается инфинитным. Описанное явление прохождения частицы через потенциальный барьер называется туннельным эффектом.

В то же время существует вероятность отражения от барьера частицы, энергия которой больше высоты барьера - эффект надбарьерного отражения.

Теперь рассмотрим некоторые свойства решений стационарного уравнения Шредингера. Оператор Гамильтона в одномерном случае имеет вид:

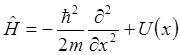,                                  (2.1)

а уравнение Шредингера можно представить следующим образом:

,                                          (2.2)

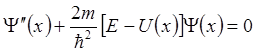
где штрихи обозначают дифференцирование по координате. Заметим, что уравнение (2.2) является действительным, поэтому у него всегда существуют решения в виде действительных функций. В случае финитного движения функции должны быть действительными, а состояния системы оказываются невырожденными (см. семинар 1). Как обычно, потребуем, чтобы волновая функция была конечной, непрерывной и однозначной на всей числовой оси . Обычно к упомянутым требованиям добавляется также условие непрерывности первой производной от волновой функции. Укажем без доказательства на следующее важное свойство состояний дискретного спектра: число узлов волновых функций  этих состояний определяется их номером. При этом волновая функция основного состояния (состояния с наименьшей энергией) не имеет узлов.  При увеличении номера на единицу у волновой функции добавляется один узел, если нумеровать состояния в порядке возрастания их энергии.

Рассмотрим для потенциала изображенного на рис.1 асимптотическое поведение волновых функций на бесконечности.

При  x → ±∞, U(x) → 0 и уравнение (2.2) приобретает вид

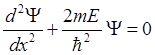                                        (2.3)

Решения уравнения зависят от знака энергии

1) Е>0 (движение инфинитное, непрерывный спектр),

            ,                                             (2.4)        где     .

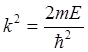Получаем два частных решения 

                                             (2.5)

Таким образом, состояния непрерывного спектра двукратно вырождены. Это вырождение связано с уже упоминавшимся в предыдущей главе свойством обратимости во времени уравнения Шредингера, при котором операция комплексного сопряжения, проведенная над волновой функцией, соответствует изменению направления времени.

2) Е<0 (движение финитное, дискретный спектр).

Уравнение запишем в виде

,                                                  (2.6)

где  .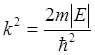                 

Волновая функция, являющаяся решением уравнения (2.6) и удовлетворяющая условию конечности, имеет вид

.                        (2.7)

Таким образом, вероятность обнаружения частицы на бесконечности стремится к нулю, что собственно и определяет финитный характер движения частицы.

Теперь перейдем к рассмотрению некоторых одномерных задач.