Исследование влияния поверхностного эффекта и эффекта близости на сопротивление токопроводов

      Санкт-Петербургский государственный

       политехнический университет

 

Кафедра теоретических основ

электротехники

Отчет по лабораторной работе № 9

Исследование влияния поверхностного эффекта и эффекта близости

 на сопротивление токопроводов

                                                                               Выполнил: Малышев П.А.

                                                                               Группа: 3026/1

                                                                               Проверил: Важнов С.А.

Санкт-Петербург

2005

Цель работы: ознакомление с методами  измерения и расчёта активного и внутреннего реактивного сопротивлений массивных токопроводов с учетом неравномерности распределения изменяющегося во времени тока по их сечению, а также уяснение зависимости этих сопротивлений от факторов, влияющих на распределение тока, таких как магнитная проницаемость, удельная проводимость материала провода, размеры поперечного сечения провода и взаимное расположение проводов.

Схема установки:

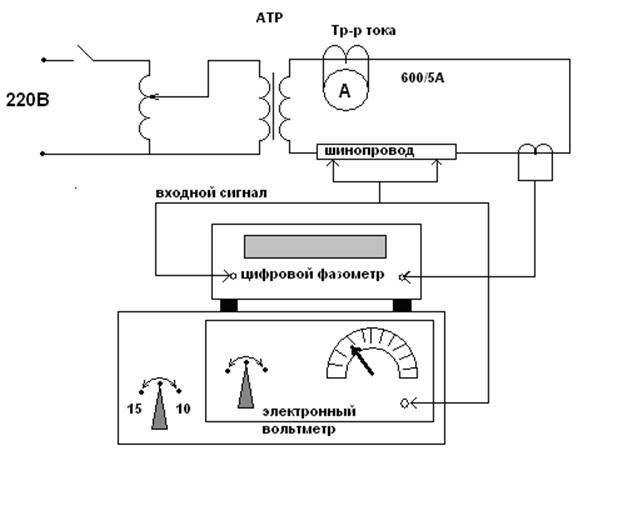
Порядок выполнения работы:

1) Определим зависимость полного сопротивления проводов двухпроводной системы из двух медных шин от расстояния между ними. При измерении полного падения напряжения, проходящего на одну шину на длине, получается:

, где U – показание вольтметра; α – показание фазометра; ψ – начальная фаза напряжения, равная углу сдвига φ между измеряемым напряжением и током в шине. Тогда полное комплексное сопротивление, приходящиеся на одну шину участка, можно вычислить по формуле:.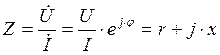

I = 540(A)

d,см	U,B	ψ,0	φ,0	r,мкОм	x,мкОм
6	13	161,7	71,7	7,6	22,9
12	18	167,4	77,4	7,3	32,5
18	21,5	169,7	79,7	7,1	39,2
30	27	171,6	81,6	7,35	49,5

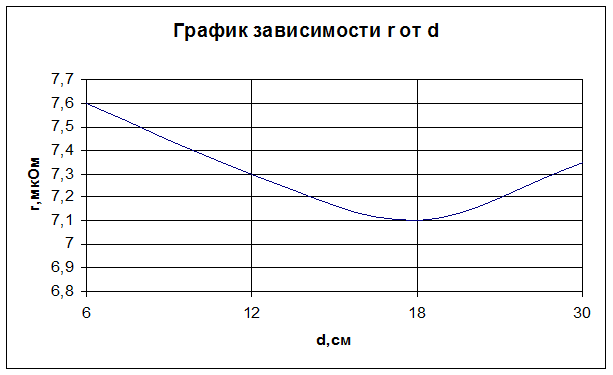
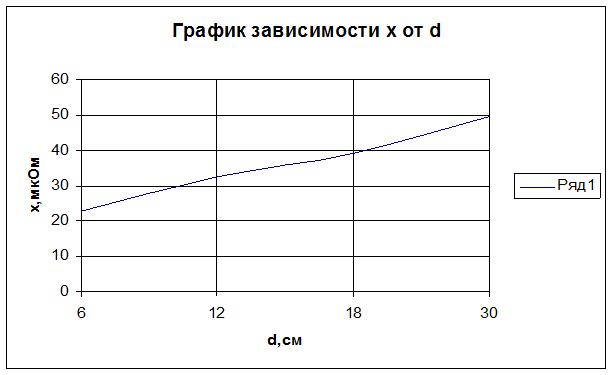
1.1) Измеренное при наибольшем расстоянии между круглыми медными шинами напряжение, приближенно определяет внутреннее сопротивление Z_i =r+j·x_i. Это значение сопоставим с рассчитанным по нижеуказанной формуле, справедливой для проводов из неферромагнитного материала и не учитывающей эффект близости:

r = Z_i·cosφ и x_i = Z_i·sinφ, причём 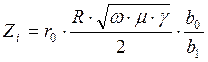, где r₀ – сопротивление провода радиуса R на постоянном токе, b₁ и b₀ – значения модулей функции Бесселя. Численные их значения можно найти в таблице, приведенной в Приложении 10 Руководства к лаборатории электромагнитного поля, рассчитав .

b₁ = 1,23

b₀ =1,38

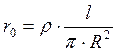
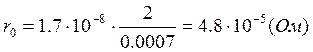
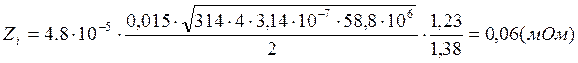
r = Z_i·cosφ = 0,06·10^-3 · cos(81,6⁰) = 8,76·10^-6  (Ом)

x_i = Z_i·sinφ= 0,06·10^-3 · sin(81,6⁰) = 59,4·10^-6    (Ом)

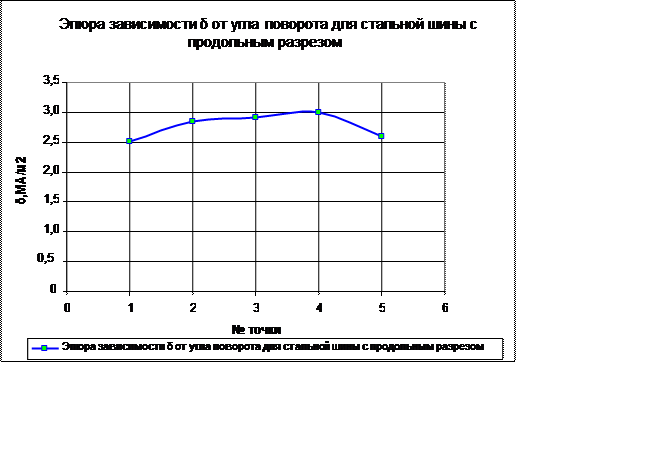
2) Исследование распределения тока по поверхности трубчатой стальной шины с продольным разрезом (и без него), измерение активного и  реактивного сопротивлений этой шины.

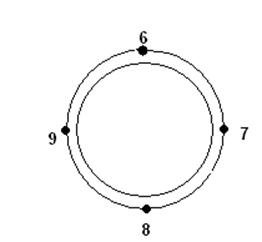
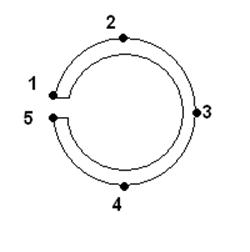
I=540 (A)

№ точки	U,мВ	ψ,0	φ,0	r,мкОм	x,мкОм	δ,МА/м2
1	63	121,2	31,2	99,8	60,4	2,52
2	71	125,8	35,8	106,6	76,9	2,84
3	73	127,5	37,5	107,2	82,3	2,92
4	75	128,4	38,4	108,8	86,3	3,0
5	65	122,3	32,3	101,7	64,32	2,6
6	90	296	26	149,8	73,06	3,6
7	90	294,2	24,2	152	68,32	3,6
8	90	293,5	23,5	153	66,46	3,6
9	90	294,5	24,5	152	69,12	3,6

2.1)В случае проводов из ферромагнитного материала формулы: 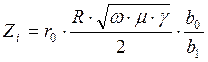, r = Z_i·cosφ и x_i = Z_i·sinφ - не даёт правильных результатов, так как при их выводе было положено, что μ =const, то есть не были учтены непостоянство магнитной проницаемости и потери на гистерезис. При резком проявлении поверхностного эффекта сопротивления r и x_i следует рассчитывать по формуле:

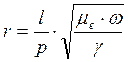   и   x_i = 0.6·r, где μ_e – магнитная проницаемость материала на поверхности провода, определяемая по основной кривой намагничивания при значениях напряжённости магнитного поля на поверхности, которая находиться, как H = I/p(I-действующее значения тока в шине, а p-величина внешнего периметра её поперечного сечения).

Рассчитаем сопротивления r и x_i для стальной шины без разреза:

p =2·π·D/2, где D- внешний диаметр стальной шины.

p =2·3,14·8,3/2 =0,522(м)

ток протекающий по шине равен: I = 540(А)

H = I/p=1040(А/м);

по основной кривой намагничивания определяем магнитная проницаемость материала на поверхности провода: μ_e/μ₀=845. тогда

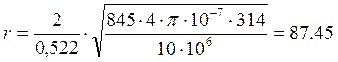(мОм)

x_i = 0.6·87,45 =52,47(мОм)

Рассчитаем сопротивления r и x_i для стальной шины с разрезом:

p = 2·π·D₁/2 + 2·π·D₂/2 + 2·h - 2·z, где D₁- внешний диаметр стальной шины, D₂- внутренний диаметр стальной шины, z - ширина разреза, h - ширина стенки стальной шины.

h = 0.65(см) ; z=0,9(см); D₁ =8,3(см); D₂ =7,65(см);

p =2·3,14·8,3/2 + 2·3,14·7,65/2 + 2·0,65 - 2·0,9 =0,513(м)

ток протекающий по шине равен: I = 540(А)

H = I/p=1053(А/м);

по основной кривой намагничивания определяем магнитная проницаемость материала на поверхности провода: μ_e/μ₀=838. тогда

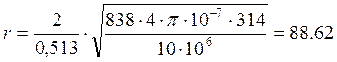(мОм)

x_i = 0,6·88,62 =53,17(мОм)

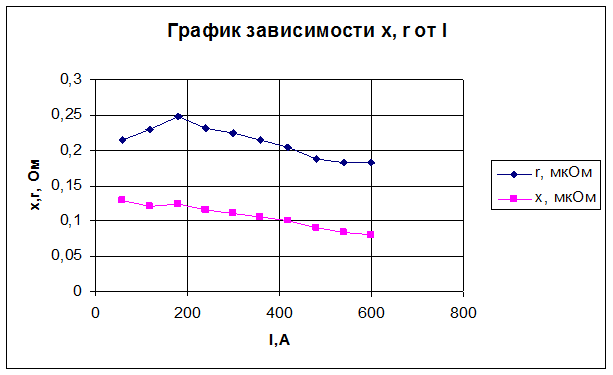
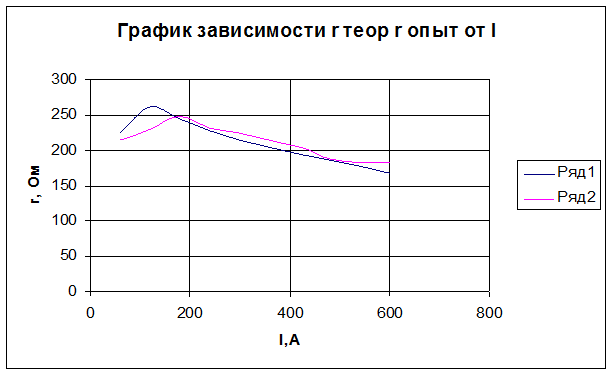
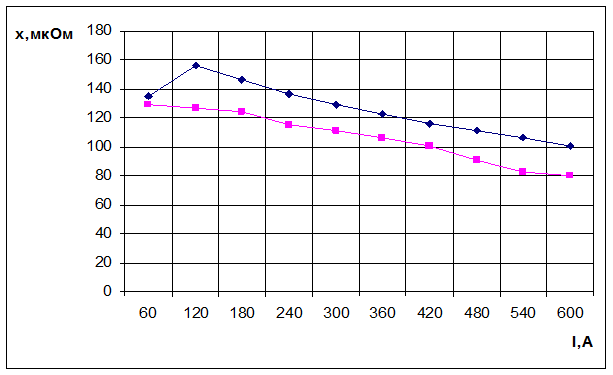
3)  Исследование зависимости активного и внутреннего реактивного сопротивлений стальной шины трубчатого сечения от действующего значения тока в ней.

I,А	U,мВ	α,°	Ψ,°	r, мкОм	x, мкОм
600	120	293.7	23.7	0.183	0.08
540	110	296	26	0.183	0.083
480	100	295.9	25.9	0.187	0.091
420	96	296.2	26.2	0.205	0.101
360	86	296.2	26.2	0.214	0.106
300	75	296.3	26.3	0.224	0.111
240	62	296.4	26.4	0.231	0.115
180	50	296.6	26.6	0.248	0.124
120	31	297.72	27.72	0.229	0.127
60	15	301.1	31.1	0.214	0.129

Теория					Эксперимент
I, А	H, А/м	μ/μo	r, мОм	x, мОм	r, мОм	x, мОм
60	229,89	877,37	225,00	135	214	129
120	459,77	1183,00	261,00	156,6	229	127
180	689,66	1036,00	244,00	146,4	248	124
240	919,54	898,29	228,00	136,8	231	115
300	1149,00	801,77	215,00	129	224	111
360	1379,00	719,93	204,00	122,4	214	106
420	1609,00	655,78	194,00	116,4	205	101
480	1839,00	598,78	186,00	111,6	187	91
540	2069,00	541,68	177,00	106,2	183	83
600	2299,00	487,90	168,00	100,8	183	80