Определение значений физических величин и установление между ними количественных соотношений (Лабораторная работа № Ф-01-00)

имеют одинаковую точность, отличаясь лишь множителем 103.

В больших числах нули справа могут служить как для указания значащих цифр, так и для определения разряда числа. Так, число 689 000 в указанной записи может иметь от трех до шести значащих цифр. Поэтому большие числа рекомендуется представлять в виде числа порядка единицы с соответствующей степенью числа 10. Указанное выше число следует записать в виде 6,89·105 , если оно имеет три значащие цифры, или 6,8900·105 , если оно имеет пять значащих цифр. Таким же образом следует записывать и малые числа: 0,00204 = 2,04·10-3 . Указанное правило облегчает вычисления с  большими и малыми числами.

Таблица 3

Примеры погрешностей округления некоторых чисел

Пример	Число значащих цифр	Погрешность округления
3,1416	5	0,00005
3,14	3	0,005
0,1500	4	0,00005
0,015	2	0,0005
3 (целое)	¥	0,000...0...

Таблица 4.

Максимальная       относительная       погрешность    чисел

с различной точностью записи

Число значащих цифр	Макс. относит. погрешность
2	0.05, (5% )
3	0.005, (0.5% )
4	0.0005, (0.05% )

Сформулируем основные правила вычислений:

1. Вычисления следует производить с таким числом значащих цифр, чтобы точность вычислений была на порядок выше точности измерений. Точность вычислений ограничивается числом с наименьшим числом значащих цифр. Целые числа считаются заданными абсолютно точно (т.е. с бесконечным числом значащих цифр).

2. Необходимое число значащих цифр должны иметь и табличные величины. В противном случае при расчете погрешностей следует учитывать неточность задания этих величин.

3. В промежуточных вычислениях число значащих цифр не должно превышать более чем на единицу число значащих цифр исходных данных, так как лишние значащие цифры, появившиеся при расчете, не повышают точности вычислений.

4. После окончания вычислений точность записи необходимо  привести в соответствие с погрешностями измерений. Так, в записи числа 20,22±0,2 указывать сотые бессмысленно, поскольку  уже десятые содержат погрешность.

5. Величина погрешности округляется до одной значащей цифры. Все расчеты погрешностей достаточно вести с двумя значащими цифрами. Иногда в записи погрешности оставляют две значащие цифры, если округление до одной значащей цифры заметно изменяет величину числа. (Например, округление погрешности  0,149 до  0,1 - первая значащая цифра равна единице).

6. Результат расчета измеряемой величины следует округлить  так, чтобы его последний десятичный разряд соответствовал последнему разряду погрешности.

Пример.     (3,8253 ± 0,032 ) - промежуточный результат и

(3,83 ± 0,03 ) - окончательный результат.

Таблица 5

Примеры записи результата

Правильно:	Неправильно:	Ошибка:
1,2± 0,2	1,244± 0,2	Лишние цифры в значении результата.
1,24± 0,03	1,2438± 0,0325	Лишние цифры в значении погрешности.
1,244± 0,014	1,244 ±0,01	Грубое округление  погрешности.
1,24 ±0,03	1,24 ±3×10-2	Множитель 10n  должен быть общим.

Графическое представление результатов.

Часто зависимость между двумя величинами выражается при помощи графиков (графически). Графики позволяют наглядно представить функциональную зависимость двух величин. При исследовании графической зависимости следует  прежде  всего обратить внимание на следующие основные особенности.

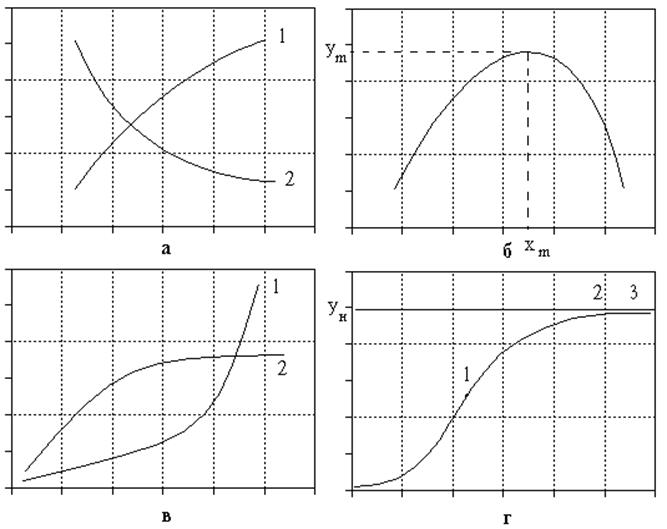Рис.1. Различный характер изменения функции: а - возрастающая (1) и убывающая (2) зависимости; б - экстремальный характер зависимости; в - скорость изменения функции возрастает (1), убывает (2); г - наличие точки перегиба (1) и участка насыщения (2 -3).

1. Характер изменения функции. Зависимость может быть возрастающей, убывающей (рис. 1,а), а также экстремальной (рис.1,б). В последнем случае следует отметить экстремальные значения переменных.

2. Скорость изменения функции может возрастать или убывать (рис.1,в) или проходить через экстремум (в точке перегиба- рис. 1, г). Участок насыщения характеризуется тем, что скорость изменения функции уменьшается практически до нуля.

Правила построения графиков. При построении графиков следует придерживаться следующих основных правил.

1. Необходимо правильно выбрать форму представления функциональной зависимости. Например, проводимость полупроводников l зависит от температуры T следующим образом:

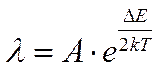
График этой зависимости достаточно сложен. Но если прологарифмировать эту зависимость,  то легко видеть, что lnl связан с величиной